Question

How do you graph `y=|x-1| +4`?

Answer 1

See the explanation below

Explanation:

Start by graphing

`y=|x|`

The function is defined for `x in RR`

`y=0` when `x=0`

When `x>0`, `y=x`

and

When `x<0`, `y=-(x)=-x`

graph{|x| [-7.15, 8.654, -0.39, 7.51]}

Next graph,

`y=|x-1|`

The graph of `y=|x|` is shifted one unit to the right

graph{|x-1| [-7.15, 8.654, -0.39, 7.51]}

And finally, graph

`y=|x-1|+4`

The graph `y=|x-1|` is shifted vertically by `4` units.

graph{|x-1|+4 [-7.15, 8.654, -0.39, 7.51]}

Answer 2

Your graph should look like:

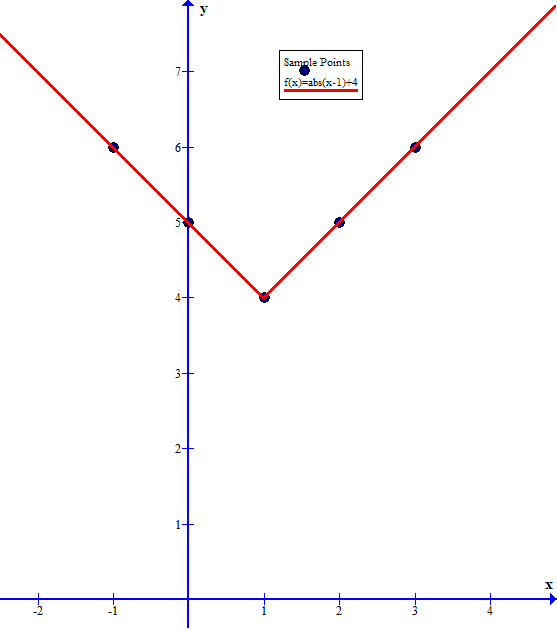
Explanation:

Generate a few sample points,
one for which `abs(x-1)=0`
and a couple for each of
`color(white)("XXX")(x-1) < 0color(white)("xx")"and"color(white)("xx")(x-1) > 0`

The sample points I used were
#color(white)("XXX"){: (color(white)("x")ul(x),color(white)("xxxx"),ul(y=abs(x-1)+4)), (color(white)("x")1,,color(white)("xxx")4), (color(white)("x")0,,color(white)("xxx")5), (-1,,color(white)("xxx")6), (color(white)("x")2,,color(white)("xxx")5), (color(white)("x")3,,color(white)("xxx")6) :}#

Plot these points on the Cartesian plane
and draw straight lines extending from the vertex point (where `abs(x-1)=0`) through each of the two sets of points.