Question

How do you graph `y=(x^3+27)/(3x^2+x)` using asymptotes, intercepts, end behavior?

Answer 1

See below.

Explanation:

`y` axis intercepts occur when `x=0`

`y=((0)^3+27)/(x(0)^2+(0))=0`

(This is undefined, so no y axis intercept)

`x` axis intercepts occur when `y=0` i.e. when `x^3+27=0`

`x^3+27=0=>x=root(3)(-27)=-3`

(This will also have complex roots, but these will be of no help in graphing).

Point: `(-3 , 0)`

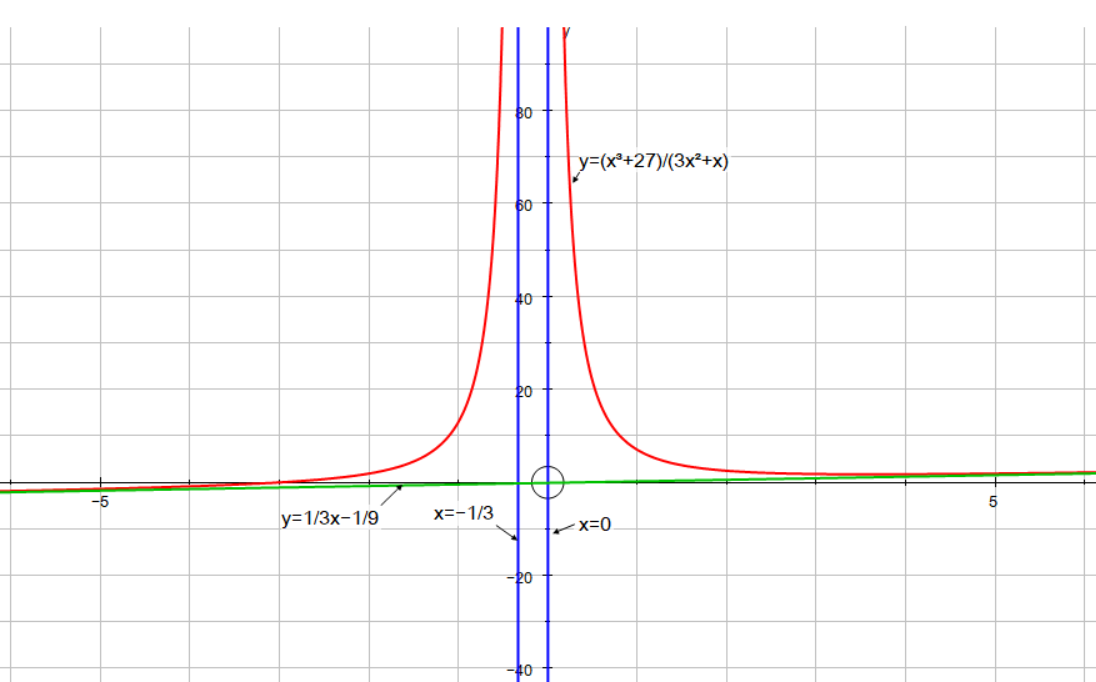
Vertical asymptotes occur where the function is undefined. i.e. `3x^2+x=0`

`3x^2+x=x(3x+1)=0=>x=0 and x=-1/3`

Asymptotes are the lines:

`color(blue)(x=0) and color(blue)(x=-1/3)`

Because the rational function is an improper fraction ( degree of numerator is higher than degree of denominator) an oblique asymptote occurs. The can be found by dividing numerator by denominator.

`(x^3+27)/(3x^2+x)=1/3x-1/9`

( we only need to divide enough to give us the terms of a line equation)

So the line:

`color(blue)(y=1/3x-1/9)` is an oblique asymptote:

End behaviour:

`x^3/(3x^2)=1/3x`

as `x->oo`,`color(white)(88)1/3x->oo`

as `x->-oo`,`color(white)(88)1/3x->-oo`

Graph: