Question

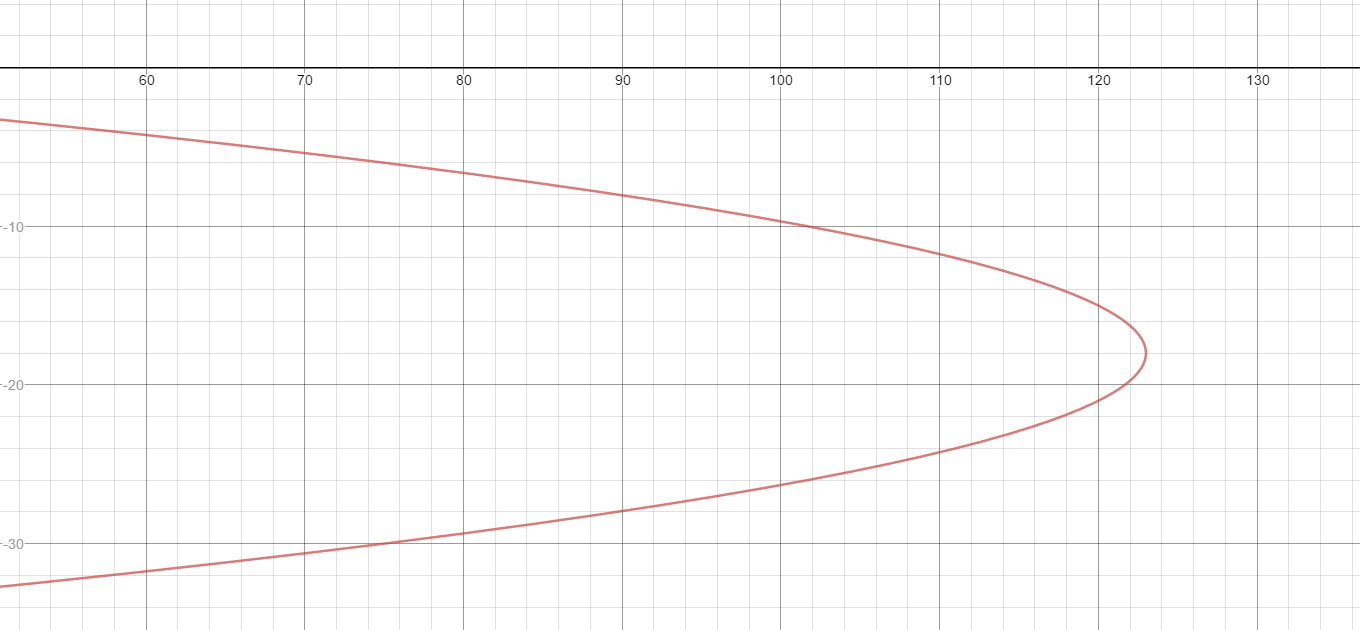
How do you identify the vertex, focus, directrix and the length of the latus rectum and graph `x=-1/3y^2-12y+15`?

Answer 1

Please see the explanation.

Explanation:

Given: `x = -1/3y^2 - 12y + 15`

To begin the conversion to the vertex form, `x = a(y - k)^2 + h`, we add 0 to the equation in the form `-1/3k^2 + 1/3k^2`:

`x = -1/3y^2 - 12y - 1/3k^2 + 1/3k^2 + 15`

Remove a factor of `-1/3` from the first 3 terms:

`x = -1/3(y^2 + 36y +k^2) + 1/3k^2 + 15`

Set the middle term in the right side of the pattern `(y - k)^2 = y^2 - 2ky + k^2` equal to the middle term in the equation:

#-2ky = 36y

`k = -18`

Substitute the left side of the pattern for the terms inside the ()s:

`x = 1/3(y - k)^2 - 1/3k^2 + 15`

Substitute -18 for k:

`x = 1/3(y - -18)^2 + 1/3(-18)^2 + 15`

Combine the constant terms:

`x = 1/3(y - -18)^2 + 123`

The vertex is at `(123, -18)`

Use `a = 1/(4f)`

`-1/3 = 1/(4f)`

`f = 1/(4(-1/3))`

`f = -3/4`

Find the focus by adding `f` to the x coordinate of the vertex:

Focus: `(122.25, -18)`

The directrix is a vertical line the same distance in the opposite direction:

`x = 123.75`

Let L = the length of the latus rectum

`L = 4|f|`

`L = 3`

Here is the graph: