How do you identity if the equation #x^2-y^2+8x=16# is a parabola, circle, ellipse, or hyperbola and how do you graph it?
1 Answer
The given equation fits the general Cartesian form of a conic section:
where
In the section entitled, Discriminant, the reference tells us to compute
The result is
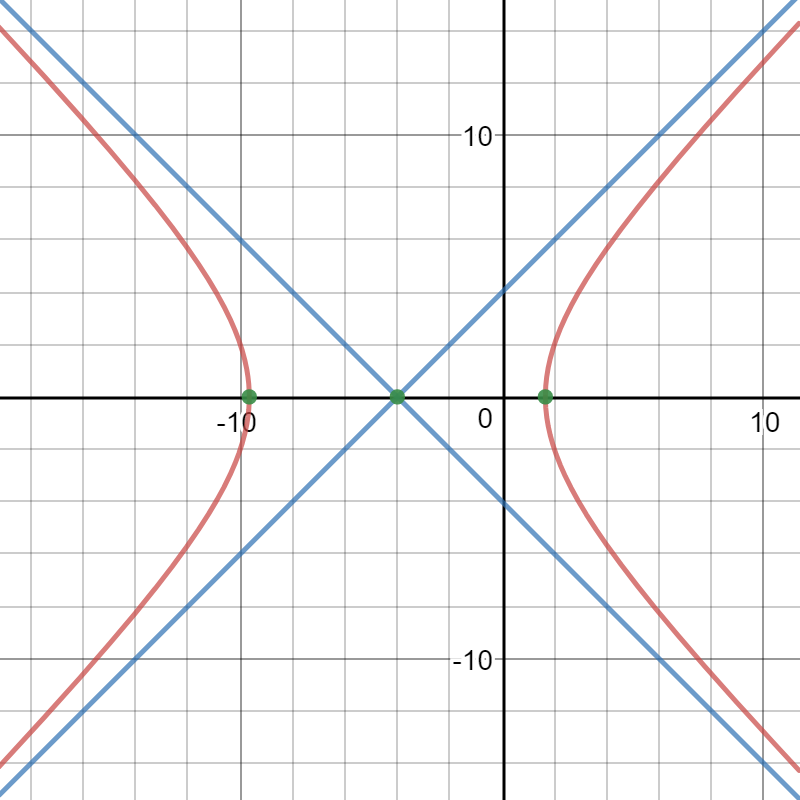
To graph the hyperbola, I recommend that you write the equation in a form that gives you, the center, the vertices and the equations of the asymptotes:
center:
vertices:
asymptotes:
Let's work on that form.
Add
The expansion of the pattern
The absence of a y term tells us that
Substitute the left side of the pattern into the equation:
Substitute the values for h and k into the equation:
Simplify
Divide both sides by 32:
Write the denominators as squares:
The center is
The vertices
The equation of the asymptotes are:
Here is a graph with the equation, the center, the vertices and the asymptotes: