Question

How do you integrate `int 1/sqrt(4x^2+12x-16)` using trigonometric substitution?

Answer 1

`1/2ln|(sqrt(4x^2 + 12x - 16) + 2x + 3)/5| + C`

Explanation:

Start by factoring the denominator.

`int 1/sqrt(4(x^2 + 3x - 4))dx`

`int1/(2sqrt(x^2 + 3x - 4))dx`

`1/2int1/sqrt(x^2 + 3x - 4)dx`

Now complete the square in the denominator.

`1/2int 1/sqrt(1(x^2 + 3x + 9/4 - 9/4) - 4)dx`

`1/2int 1/sqrt(1(x + 3/2)^2 - 9/4 - 4)dx`

`1/2int 1/sqrt((x + 3/2)^2 - 25/4)dx`

Now let `u = x + 3/2`: Then `du = dx`.

`1/2int 1/sqrt(u^2 - 25/4)du`

Apply the substitution `u = 5/2sectheta`. Then `du = 5/2secthetatantheta d theta`:

`1/2int 1/sqrt((5/2sectheta)^2 - 25/4)* 5/2secthetatantheta d theta`

`1/2int 1/sqrt(25/4sec^2theta - 25/4)* 5/2secthetatantheta d theta`

`1/2int 1/sqrt(25/4(sec^2theta - 1))* 5/2secthetatantheta d theta`

Apply `sec^2theta -1 = tan^2theta`:

`1/2int 1/sqrt(25/4tan^2theta)* 5/2secthetatantheta d theta`

`1/2int 1/(5/2tantheta)* 5/2secthetatantheta d theta`

`1/2int sec theta d theta`

This is a known integral: `intsecxdx = ln|secx + tanx|`. For more details on how to integrate this, go [here].(http://math2.org/math/integrals/more/sec.htm)

We must determine an expression for `sectheta` and `tantheta`. Draw a triangle:

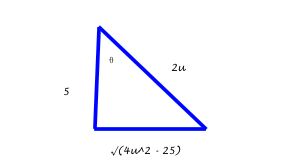
As you can see, `tantheta = sqrt(4u^2 - 25)/5` and `sectheta = (2u)/5`

`1/2ln|sqrt(4u^2 -25)/5 + (2u)/5| + C`

`1/2ln|(sqrt(4u^2 - 25) + 2u)/5| + C`

`1/2ln|(sqrt(4(x + 3/2)^2 - 25) + 2(x + 3/2))/5| + C`

`1/2ln|(sqrt(4x^2 + 12x - 16) + 2x + 3)/5| + C`

Hopefully this helps!