How do you integrate int 1/sqrt(-e^(2x) +9)dx using trigonometric substitution?
1 Answer
Explanation:
Here is the corresponding right triangle from which you can extract all the parts for substitution:
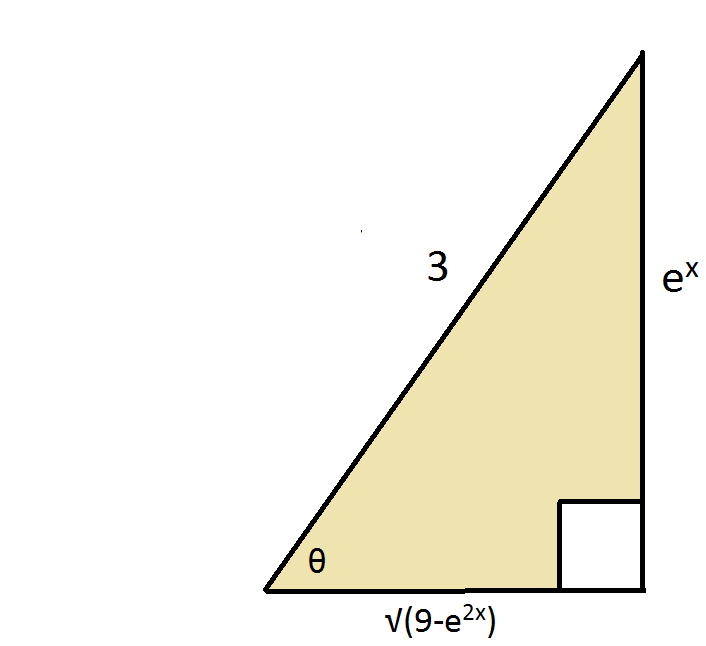
You need to find the following and then systematically replace all x terms (rectangular) with
x
I'll start you off in the right direction:
Since
We have then that:
Now differentiate with respect to
You can then rewrite that entire integrand in terms of
I'll give you one more piece and then I gotta sleep!
What is
Well, referencing the triangle you can see that:
This says that:
You'll still need to find
So now you can systematically replace all rectangular terms with
trigonometric terms.
That's your job!

