How do you integrate #int 2/(y^4sqrt(y^2-25)# using trig substitutions?
1 Answer
Explanation:
Our goal here is to get rid of the
#=int 2/((5sectheta)^4sqrt((5sectheta)^2 - 25)) * 5secthetatanthetad theta#
Apply the identity
#=int 2/(625sec^4thetasqrt(25tan^2theta))* 5secthetatantheta d theta#
#=int 2/(625sec^4(5tantheta)) * 5secthetatantheta d theta#
#=int 2/(625sec^3theta) d theta#
Rewrite using
#=int 2/625cos^3theta d theta#
#=int 2/625 cos^2theta(costheta) d theta#
Rearrange using the pythagorean identity
#=int 2/625 (1 - sin^2theta)costheta d theta#
Let
#=int 2/625 (1 - u^2)costheta * (du)/costheta#
#=int 2/625( 1 - u^2) du#
Integrate using
#=2/625(u - 1/3u^3) + C#
#=2/625sintheta - 2/1875sin^3theta + C#
Draw a triangle to represent
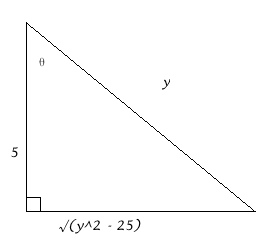
#=2/625sqrt(y^2 - 25)/y - 2/1875(sqrt(y^2 - 25)/y)^3 + C#
#=(2sqrt(y^2 - 25))/(625y) - (2(y^2-25)^(3/2))/(1875y^3) + C#
Hopefully this helps!

