How do you integrate #int (3x^3+2x^2-7x-6)/(x^2-4) dx# using partial fractions?
1 Answer
The integral is
Explanation:
Start by using long division to divide. We want the degree of the numerator to be less than the degree of the denominator.
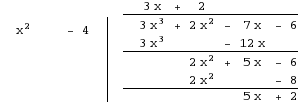 .
.
So, the quotient is
We can now write
So,
So, the partial fraction decomposition is
We rewrite the integral like this:
Integrate using the rule
You can check the answer by differentiating. You will get the initial problem.
Hopefully this helps!

