Question

How do you integrate `int x/sqrt(x^2+1)` by trigonometric substitution?

Answer 1

`sqrt(x^2 + 1) + C`

Explanation:

Let `x= tantheta`. Then `dx = sec^2thetad theta`

`=> int tan theta/sqrt((tan^2theta + 1)) sec^2theta d theta`

`=> int tantheta/sqrt(sec^2theta) sec^2theta d theta`

`=> int tantheta/sectheta sec^2theta d theta`

`=> int tan theta sec theta d theta`

This is a common integral--`int(tanxsecx)dx = secx + C`.

`=> sec theta + C`

We now draw an imaginary triangle.

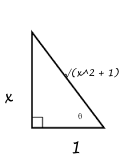
The definition of `sectheta` is `"hypotenuse"/("side adjacent" theta)` because `secx = 1/cosx`. In this image, `sectheta = sqrt(x^2 + 1)`.

Therefore, the integral can be simplified to `sqrt(x^2 + 1) + C`.

Hopefully this helps!

Answer 2

By inspection rather than trig substitution.

Explanation:

Notice that the `x` in the top is proportional to the derivative of the function under the square root. So just write down `(x^2+1)^(-1/2+1)` as a trial (rather like integrating any power of `x`) and differentiate it. By the chain rule, the function under the square root will provide the `2x` and the `2`'s will cancel, so the trial was an immediate success.

Alternatively substitute `u=x^2+1`, `dx=(du)/(2sqrt(u-1))` and the integral becomes `(1/2)int u^(-1/2)du` = `u^(1/2)+C`=`sqrt(x^2+1)+C`