Question

How do you minimize and maximize `f(x,y)=x^2-y/x` constrained to `0<x+3y<2`?

Answer 1

The intent may have been to apply derivatives, but the explanation below would seem to provide a simpler solution: `(-oo,+oo)`

Explanation:

Maximization
Note that the constraint `0 < x+3y <2`
allows `xrarr +oo` (provided `3y rarr -oo`)
In which case `f(x,y) rarr +oo`

Minimization
Note that the constraint `0 < x+3y < 2`
allows `x rarr 0+` (provided `y > 0`)
In which case `f(x,y) rarr -oo`

Answer 2

See below.

Explanation:

Given `f(x,y)=x^2-y/x` subjected to `Omega(x,y)`

`Omega(x,y) ={ (x,y) | 0 < x+3y < 2}`

We are looking for local minima/maxima.

This problem can be handled using lagrange multipliers. This can be done following the steps:

1) Describe `Omega(x,y)` through equality constraints
This can be done introducing the so called slack variables `s_1,s_2` and making

`g_1(x,y,s_1) = x + 3y - s_1^2=0`
`g_2(x,y,s_2) = x + 3y - 2+ s_2^2=0`

then `Omega(x,y) equiv g_1(x,y,s_1) nn g_2(x,y,s_2)`

2) Form the Lagrangian

`L(x,y,s_1,s_2,lambda_1,lambda_2)=f(x,y)+lambda_1g_1(x,y,s_1)+lambda_2 g_2(x,y,s_2)`

3) Determine the stationary points of `L(x,y,s_1,s_2,lambda_1,lambda_2)`

This is done computing the solution to

`grad L(x,y,s_1,s_2,lambda_1,lambda_2) = vec 0`

where `grad` represents the partial derivatives operator

`grad = (partial/(partial x),partial/(partial y),partial/(partial s_1),partial/(partial s_2),partial/(partial lambda_1),partial/(partial lambda_2))`

so the equations which define the stationary points are

#{ (lambda_1 + lambda_2 + 2 x + y/x^2= 0), (3 lambda_1 + 3 lambda_2 -1/x= 0), (2 lambda_1 s_1 =0), (2 lambda_2 s_2 = 0), ( x + 3 y-s_1^2 = 0), (x + 3 y-2 + s_2^2 = 0):}#

Solving for `x,y,s_1,s_2,lambda_1,lambda_2` we obtain the only real solution

#((f(x,y),x,y,s_1,s_2,lambda_1,lambda_2),(1.775,-0.693, 0.897., -1.414, 0,0, -0.480) )#

4) Qualifying the stationary points

This can be done computing `(d^2(f @ g_i))/(dx^2)` for `i=1,2`

and depending on the sign, if positive it is a local minimum and if negative a local maximum.

In our case,

`(f@g_1)(x) = 1/3 + x^2`
`(f@g_2)(x) =1/3 - 2/(3 x) + x^2`

`(d^2)/(dx^2)(f@g_1)(x) = 2`
`(d^2)/(dx^2)(f@g_2)(x) =2 - 4/(3 x^3)`

The evaluations must be done according to the values found for `s_1` and `s_2` so, this point shall be qualified with `(d^2)/(dx^2)(f@g_2)(x), (s_2= 0)`

Attached a plot showing the region with the objective function level curves, and the stationary point.

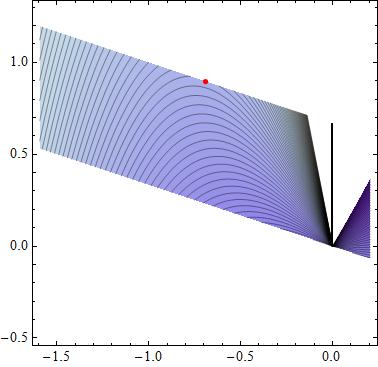
The qualification is left to the reader. I think it is a local minimum.

Note. Of course if the evaluation gives zero we will continue the qualification process but this is another chapter.