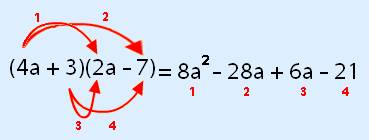How do you multiply #(3x^2 + 2x + 4)(2x + 1)#?
2 Answers
Explanation:
You have to take each number in the first bracket and multiply it by the second one.
First lets do
Then
This will give
Then
This will give
Taking all these, you simply just add them together!
Explanation:
Do the first term in the first bracket multiplied by the first term in the second bracket. Do the same with the first term in the first bracket (
(
(
[For powers, use the rule:
Then multiply any real numbers as you normally would (
For the next step, multiply the second term of the first bracket to the first of the second bracket:
(
(
Proceed to the final term in the first bracket and follow the same steps:
(
(
Simplify by adding all like terms together: