How do you multiply #(c^2t^2+1)^2#?

1 Answer
Meave60
Jul 3, 2015

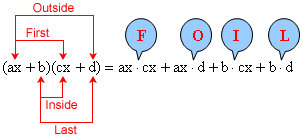
You can rewrite the expression as multiplication between two binomials, and use the FOIL method to multiply.

Explanation:

#(c^2t^2+1)^2=(c^2t^2+1)(c^2t^2+1)#

The FOIL method of multiplying indicates the order in which you multiply the terms in the binomials.

http://www.mesacc.edu/~scotz47781/mat120/notes/polynomials/foil_method/foil_method.html

#(c^2t^2+1)(c^2t^2+1)# =

#c^2t^2*c^2t^2+c^2t^2*1+1*c^2t^2+1*1c^4t^4+2c^2t^2+1# =

#c^4t^4+2c^2t^2+1#

Related questions
See all questions in Multiplication of Polynomials by Binomials
Impact of this question
1410 views around the world
You can reuse this answer
Creative Commons License