How do you multiply (x+2)^5?
3 Answers
Explanation:
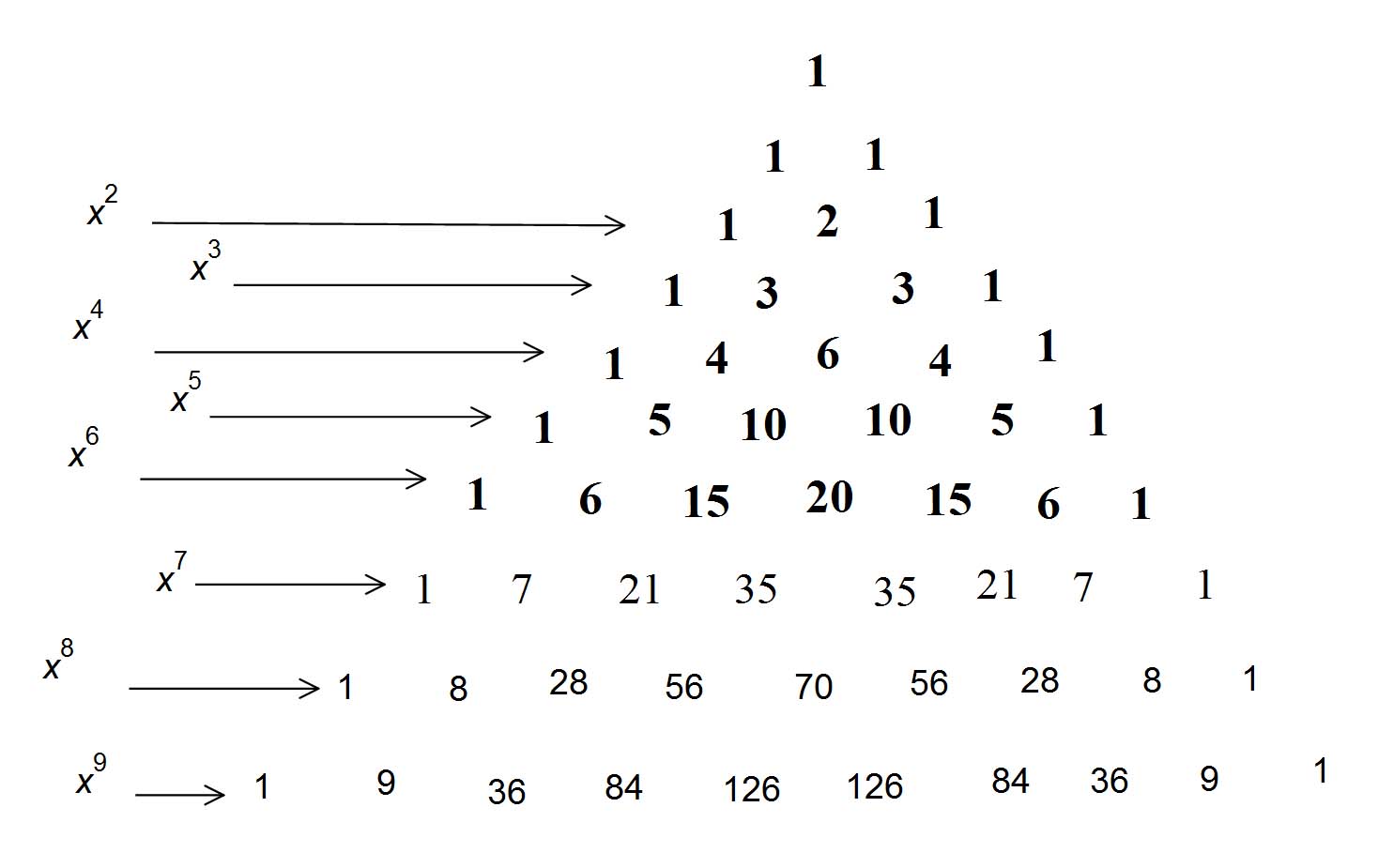
Use Pascal's triangle (n=5 so 5th row) giving you 1,5,10,10,5,1. The powers of x go from
So 1st term is 1 (from Pascal) multiplied by
2nd term is 5 multiplied by x^4 then 2^1
and so on.
In an exam, you won't have the triangle so you can use the nCr button to find the multipliers.
 Tony B
Tony B
See a solution process below:
Explanation:
We can use Pascal's triangle to solve this problem.
The triangle values for the exponent 5 are:
Therefore
You can use the Binomial Theorem to expand.
Explanation:
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
By way of explanation using 1 example
The above is called a Combination which in general terms is:
This is different to Permutations which in general terms is:




