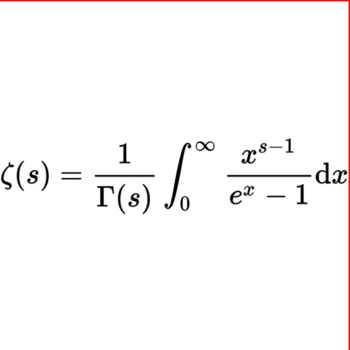How do you simplify #(2xyz)/(x^2z^2)div (6y^3)/(3xz)#?
1 Answer
Mar 2, 2017
Explanation:
When we divide one fraction with another one, we can rewrite it as multiplication of first fraction by the second one, it means:
so let's do the trick and see what'll happen
and we simply multiply the numerator by the numerator and the denominator by the denominator.
and by simplifying this fraction we get: