Question

How do you sketch the angle in standard position `-(23pi)/3`?

Answer 1

Please read the explanation.

Explanation:

Objective: Sketch the angle `(-(23pi)/3)` in the standard position.

An angle is said to be in the standard position in the Cartesian Coordinate System if it's vertex is at the origin and it's initial side lies on the positive x-axis.

`color(green)("Step 1")`

Examine the image (this was originally constructed using a computer software) given below with the angles measured in radians:

`color(green)("Step 2")`

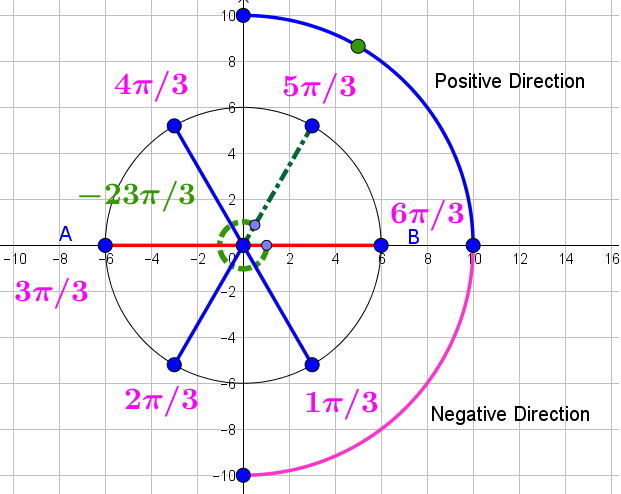
One complete rotation is `2pi` radians.

Observe that `2pi` can also be written as `(6pi)/3`.

We do this because we are sketching the angle `[-(23pi)/3]`, that has a denominator of `3`.

Now, it becomes easier to divide one full rotation into convenient slices of angles as shown in the image above.

Negative angles are measured in clockwise direction from the initial side.

`color(green)("Step 3")`

To sketch the angle `[-(23pi)/3]`, find how many full rotations it makes.

`rArr (-(23pi)/3)*(1/(2pi))`

`rArr "-23/6 rotations"`

One full rotation brings the angle back into standard position.

Hence, the angle `(-(23pi)/3)` in the image above, will take 3 full rotations and a `(5/6)^(th)` of a rotation.

Hence, we can see that the angle `(-(23pi)/3)` lies in Quadrant-1.

Hope it helps.