Question

How do you sketch the graph of `y=(x+2)^2` and describe the transformation?

Answer 1

`" "`
Please read the explanation.

Explanation:

`" "`
We are given the quadratic function: `color(red)(y=f(x)=(x+2)^2`

For the family of quadratic functions,

the parent function is of the form `color(blue)(y=f(x)=x^2`

When graphing quadratic functions, there is a useful form called the vertex form:

`color(green)(y=f(x)=a(x-h)^2+k`, where

`color(green)((h,k)` is the vertex.

Data table is given below:

(both for the parent function and the given function)

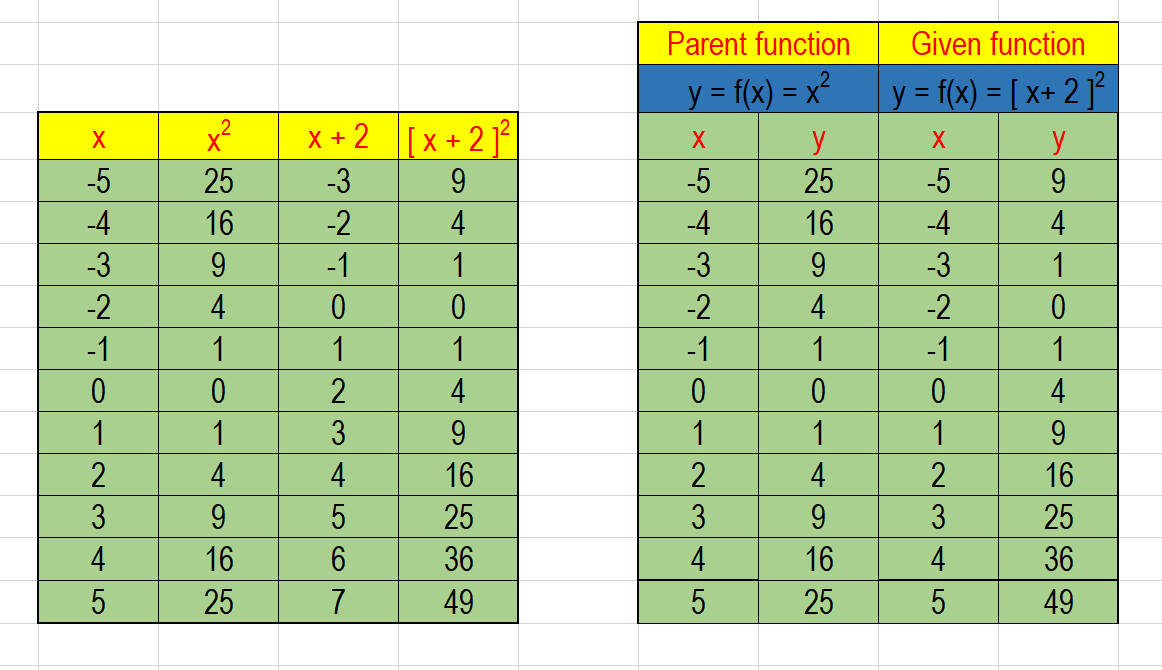
For the parent function,

Vertex: `color(red)((h,k)=(0,0)`

For the given function,

Vertex: `color(red)((h,k)=(-2,0)`

Let us graph:

`color(red)(y=f(x)=(x+2)^2`

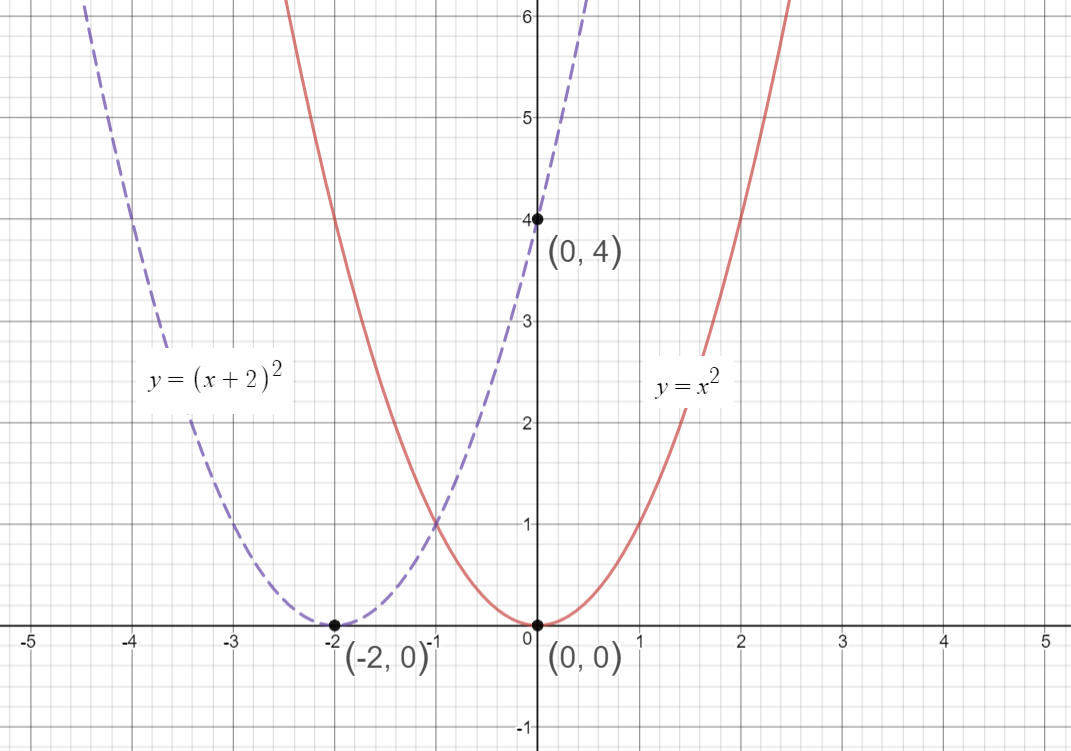
moves (shifts) the graph LEFT by 2 units.

Note on Transformation:

Hence we can observe that there is a horizontal translation.

Hope it helps.