How do you sketch the graph of #y=(x+3)^2+6# and describe the transformation?
1 Answer
Refer to the explanation.
Explanation:
First, let's look at the transformations of this equation.
When something is with the
However, when something is "outside" the
Here is the graph (should be arrows at each end, just doesn't show):
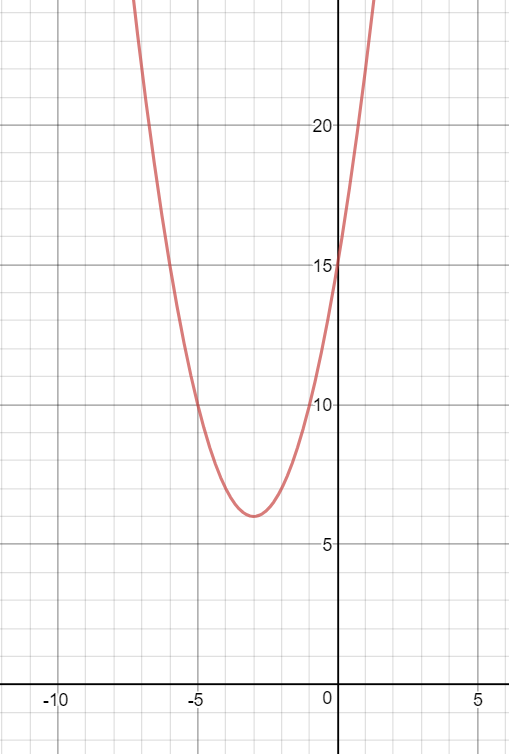
As you can see, there is a point, or the vertex, is at
When the coefficient of a quadratic equation is positive , (ex:
When the coefficient is negative, (ex:
Our coefficient is just

