How do you sketch the parabola #(x-3)^2=-16y# and find the vertex, focus, and directrix?
1 Answer
Feb 18, 2018
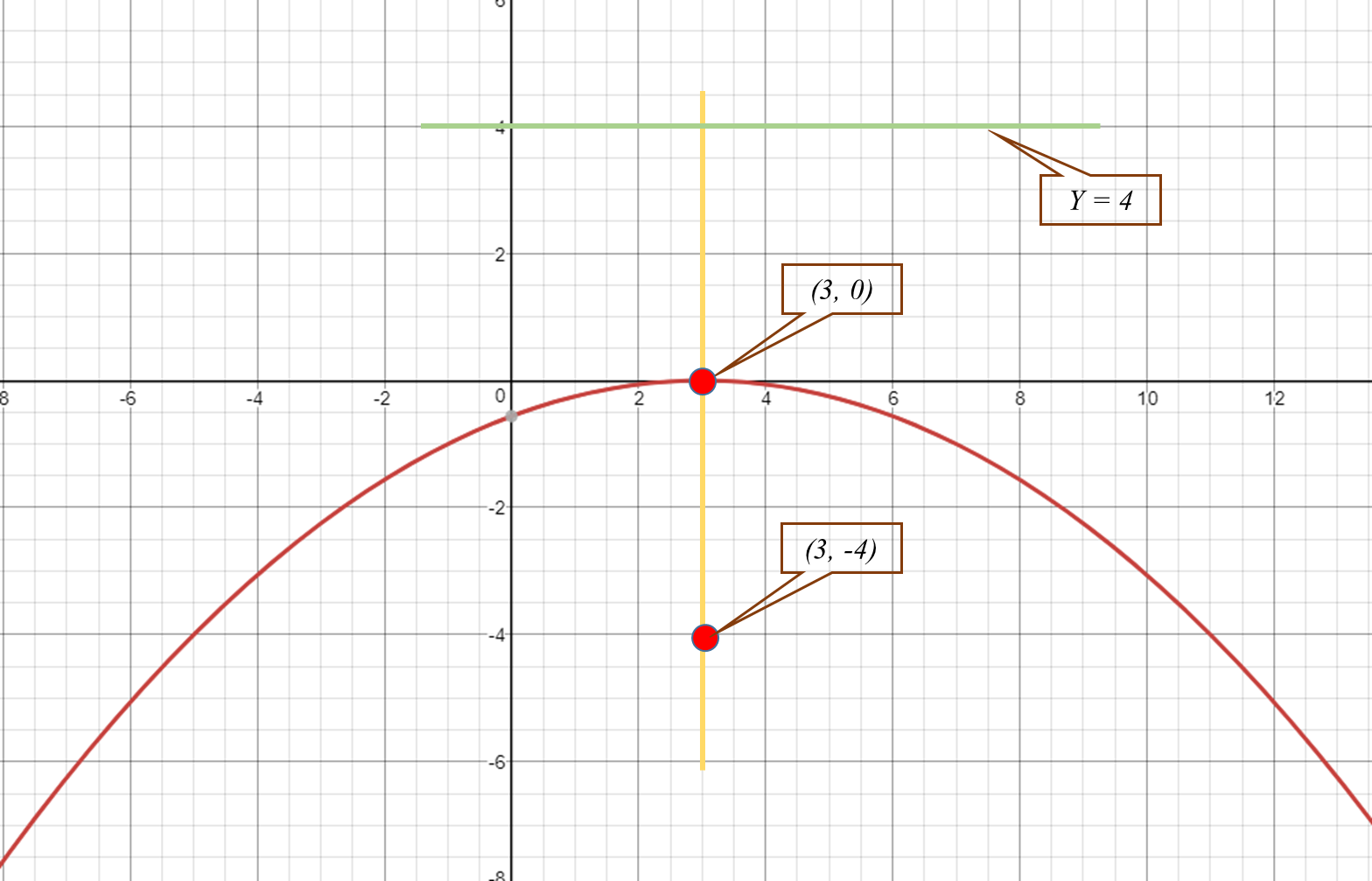
Vertex -
#(3,0)#
Focus -
#(3,-4)#
Directrix -
#y=4#
Explanation:
Given -
#(x-3)^2=-16y#
It is in the form -
#(x-h)^2=-4a(y-k)#
If it is so, then the parabola opens down, has its vertex at
We shall rewrite the given equation as -
#(x-3)^2=-4xx4xx(y-0)#
Vertex -
#(3,0)#
Focus -
#(3,-4)#
Directrix -
#y=4#

