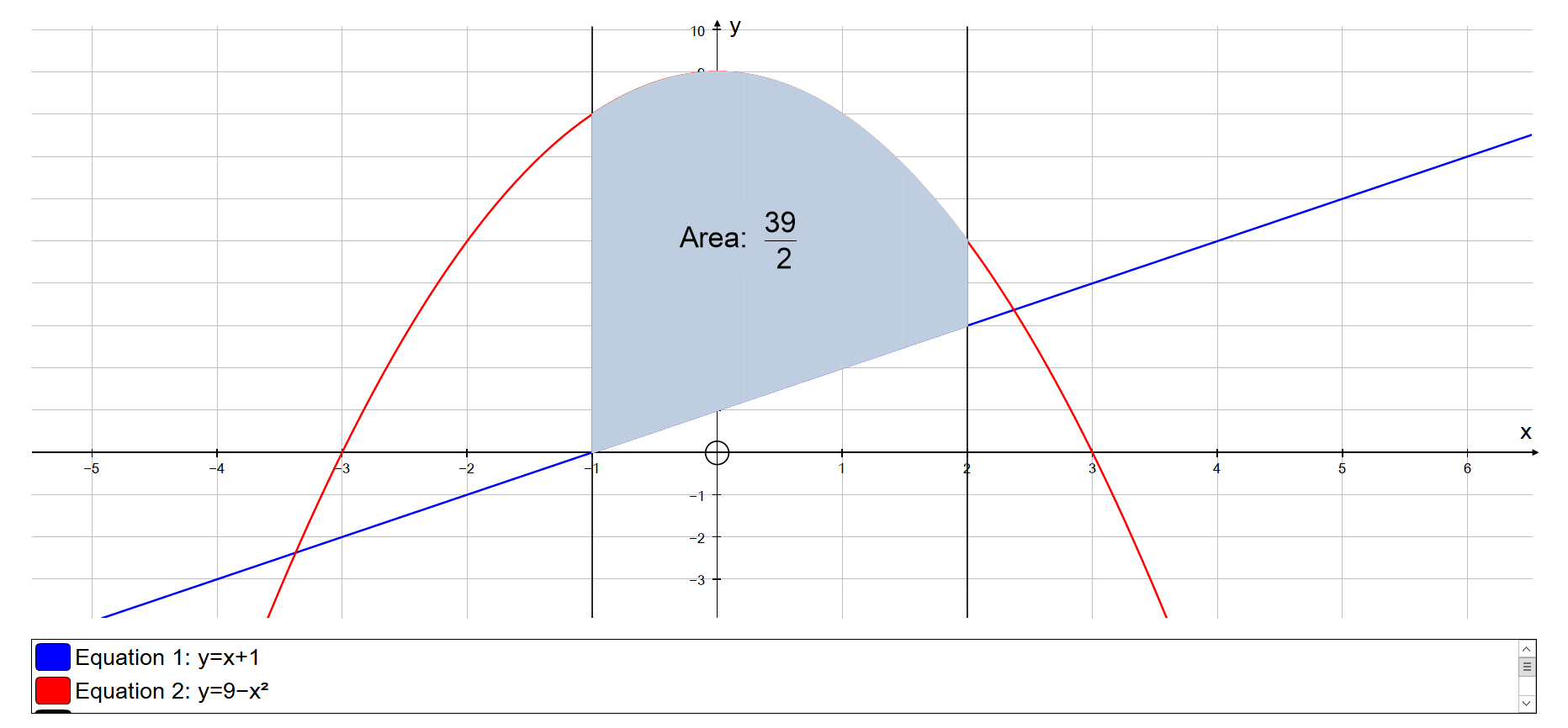
How do you sketch the region enclosed by #y=x+1, y=9-x^2, x=-1, x=2# and find the area?

Question

15796 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-03-13T14:42:25

#color(blue)(39/2)# Units squared.

If we look at the two functions in the given interval we see that:

#y=9-x^2# attains greater values than #y=x+1#. therefore #y=9-x^2# is above #y=x+1# in the given interval.

The area between these two functions in the given interval will be:

#int_(-1)^(2) (9-x^2)-(x+1) dx#

#int_(-1)^(2)(-x^2-x+8)dx=[-1/3x^3-1/2x^2+8x]_(-1)^(2)#

#"Area"=[-1/3x^3-1/2x^2+8x]^(2)-[-1/3x^3-1/2x^2+8x]_(-1)#

Plugging in upper and lowers bounds:

#=[-1/3(2)^3-1/2(2)^2+8(2)]^(2)-[-1/3(-1)^3-1/2(-1)^2+8(-1)]_(-1)#

#"Area"=[34/3]^(2)-[-49/6]_(-1)=color(blue)(39/2)# Units squared.

GRAPH:

enter image source here