How do you solve #1/3x^2 - 3=0# by graphing?

Question

2979 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-07-06T02:52:22

Refer the Explanation section

Given -

#1/3 x^2-3=0#

We shall have it as -

#y=1/3 x^2-3#

To graph the function, we must have the range of x values the includes solutions.

Find the two x-intercepts first

At #y=0; 1/3x^2-3=0#

#x^2=-=3 xx 3/1=9#

#x=+-sqrt9#
#x=3#
#x=-3#

The curve cuts the x-axis at #(3,0);(-3,0)#

Now take #x# values ranging from # 5 # to # -5#
Find the corresponding #y# values.
enter image source here

Then plot these values on a graph sheet.

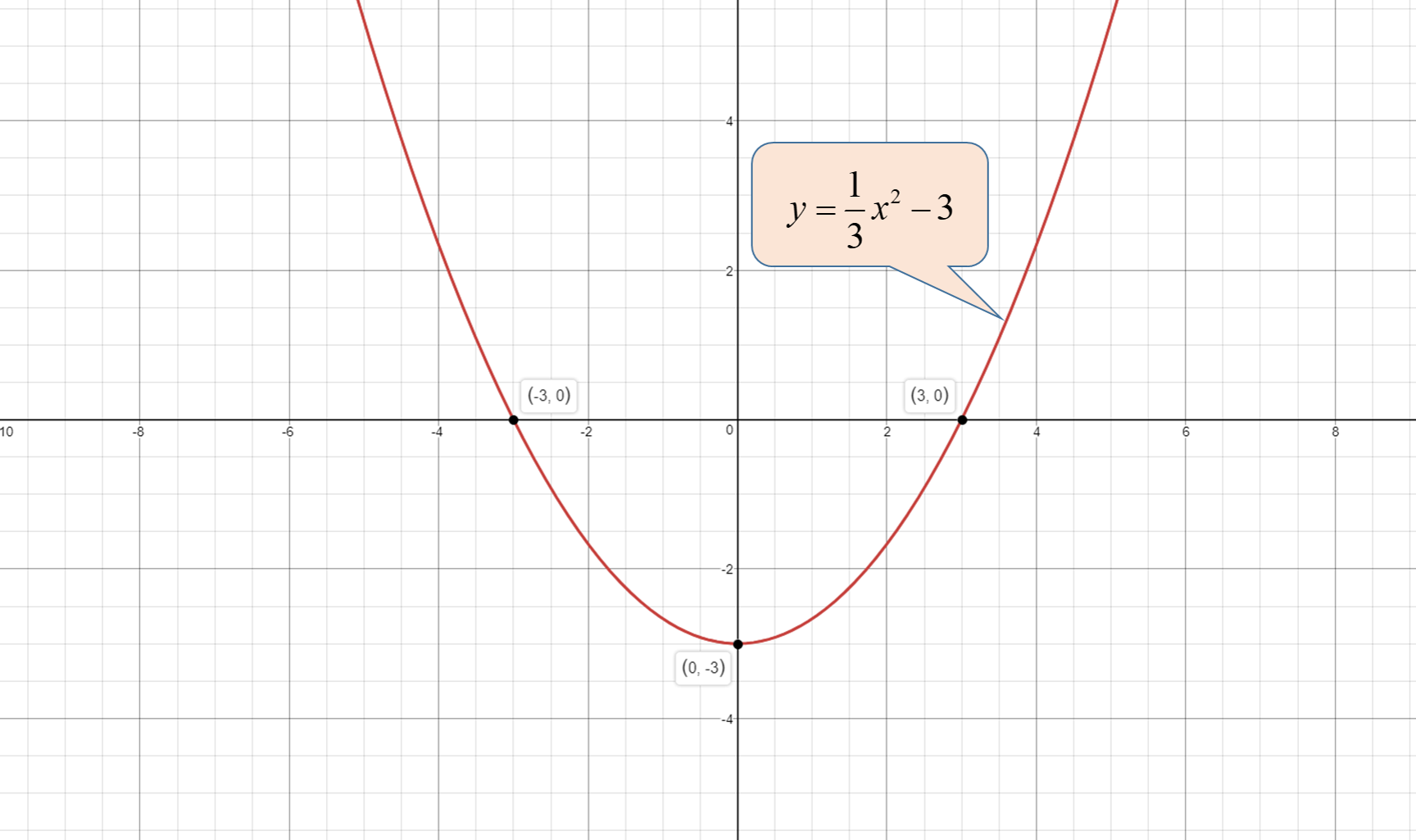
enter image source here

Answer 2 · 2017-07-06T03:02:01

Plot the graph of #f(x) = 1/3x^2-3#. Solutions for #x# are found where #f(x)# intercepts the #x-#axis. #x=+-3#

The graph of #f(x) = 1/3x^2-3# is shown below.

graph{1/3x^2-3 [-7.023, 7.024, -3.51, 3.513]}

From this graph we can observe the #f(x)=0# for #x=+-3#

Hence this is the answer to this question.

We can, of course, solve the equation algebraically to prove this observation.

#1/3x^2-3=0 -> 1/3x^2 = 3#

#:.x^2=3xx3 = 9#

#x=sqrt9 =+-3#