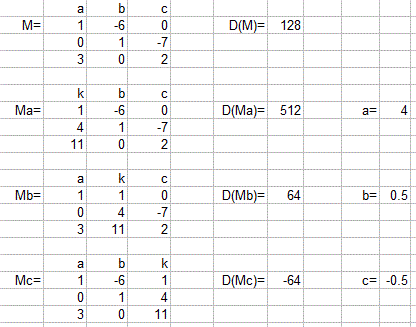Let #X=((a),(b),(c))#
Using Cramer's Rule to solve the augmented matrix
#color(white)("XXXXXXXXXXXxX")acolor(white)("XX")bcolor(white)("Xx")c color(white)("XXX")k#
#color(white)("XXX")((M,"|",k))=((1,-6,0,"|",1),(0,1,-7,"|",4),(3,0,2,"|",11))#
Calculating the Determinants:
#color(white)("XXX")Det(M)= |(1,-6,0),(0,1,-7),(3,0,2)|#
#color(white)("XXXXXXX")=1color(white)("X")[(1xx2)-(0xx-7)]#
#color(white)("XXXXXXXX")-color(white)("X")0[(-6xx2)-(0xx0)]#
#color(white)("XXXXXXXX")+3color(white)("X")[((-6)xx(-7))-(0xx0)]#
#color(white)("XXXXXXX")=128#
Similarly
#color(white)("XXX")Det(M_a)=512#
#color(white)("XXX")Det(M_b)=64#
#color(white)("XXX")Det(M_c)=-64#
By Cramer's Rule:
#color(white)("XXX")a=(Det(M_a))/(Det(M))=512/128=4#
#color(white)("XXX")b=(Det(M_b))/(Det(M))=64/128=0.5#
#color(white)("XXX")c=(Det(M_c))/(Det(M))=(-64)/128=-0.5#
Confession: I used as spreadsheet to do the detailed arithmetic work