Cramer's Rule
Key Questions
-
Cramer's rule is used to solve a square system of linear equations, that is, a linear system with the same number of equations as variables. In a square system, you would have an
#nxx(n+1)# matrix.So you should have a
#2xx3# matrix in order to use Cramer's rule. A#2xx2# matrix would only have the coefficients of the variables; you need to include the constants of the equations. -
You divide each variable determinant by the determinant of the coefficients.
EXAMPLE:
Use Cramer's Rule to solve the following system of equations:
#2x+y+z=3#
#x–y–z=0#
#x+2y+z=0# Solution:
The left hand side gives us the coefficient matrix.
#((2,1,1),(1,-1,-1),(1,2,1))# The right hand side gives us the answer matrix.
#((3),(0),(0))# The determinant
#D# of the coefficient matrix is#D = |(2,1,1),(1,-1,-1),(1,2,1)| = -2+2-1+1-1+4=3# Let
#D_x# be the determinant formed by replacing the#x# -column values with the answer-column values:#D_x=|(3,1,1),(0,-1,-1),(0,2,1)|= -3+6=3# Similarly,
#D_y=|(2,3,1),(1,0,-1),(1,0,1)|= -3-3=-6# and
#D_z=|(2,1,3),(1,-1,0),(1,2,0)| = 6+3=9# Cramer's Rule says that
#x = D_x/D =3/3=1# ,#y = D_y/D=-6/3=-2# ,#z = D_z/D=9/3=3# .The solution is
#x=1,y=-2,z=3# -
Answer:
It is useful when you just want to find the value of 1 unknown in a system of linear equations without needing to find all the unknowns.
Explanation:
To find just 1 unknown in a system of linear equations you need to find only 2 matrix determinant values and then use Cramer's Rule
-
Cramer's Rule.
This rule is based upon manipulation of determinants of the matrices associated with the numerical coefficients of your system.You just pick the variable you want to solve for, replace that variable's column of values in the coefficient determinant with the answer-column's values, evaluate that determinant, and divide by the coefficient determinant.
It works with systems with a number of equations equal to the number of unknowns. it also works well up to systems of 3 equations in 3 unknowns. More than that and you´ll have better chances using reductions methods (row echelon form).
Consider an example:

(NOTE: if#det(A)=0# you cannot use Cramer's Rule and your system will not have a unique solution).Now we consider 3 other matrices,
#A_x, A_y and A_z# and their determinant. These matrices are obtained by substituting each column of#A# with the answer-column's values (the ones without unknown):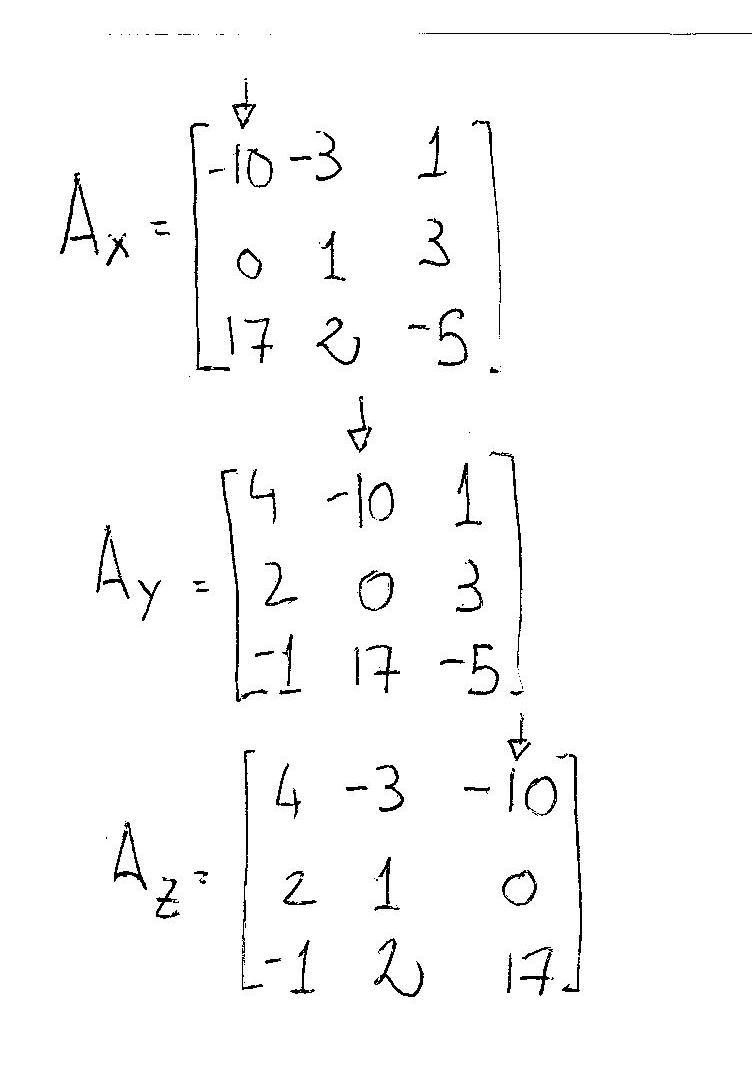
We evaluate the three determinants for these matrices:
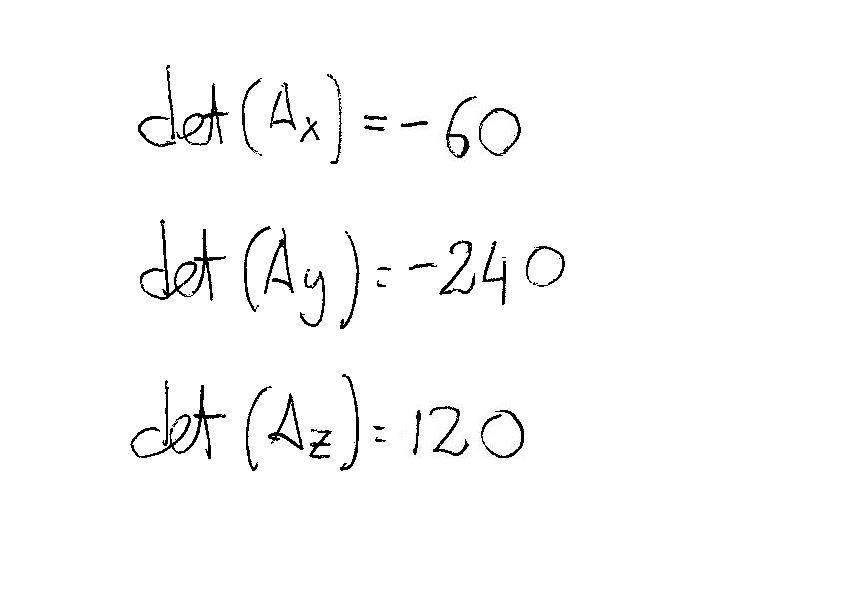
Finally we can calculate the values of the unknowns as:
#x=det(A_x)/(det(A))=(-60)/-60=1#
#y=det(A_y)/(det(A))=(-240)/-60=4#
#z=det(A_z)/(det(A))=(120)/-60=-2# Your final result is:
#x=1#
#y=4#
#z=-2#