How do you solve #12<-4(3c-6)# and graph the solution on a number line?

Question

2208 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-07-24T18:34:44

#c < 1#

#12 < -4(3c-6)#

Distribute the right side:
#12 < -12c + 24#

Add #color(blue)(12c)# to both sides:
#12 quadcolor(blue)(+quad12c) < -12cquad + quad24 quadcolor(blue)(+quad12c)#

#12 + 12c < 24#

Subtract #color(blue)(12)# from both sides:
#12 + 12c quadcolor(blue)(-quad12) < 24 quadcolor(blue)(-quad12)#

#12c < 12#

Divide both sides by #color(blue)12#:
#(12c)/color(blue)12 < 12/color(blue)12#

#c < 1#

Here is a graph of it on a number line:
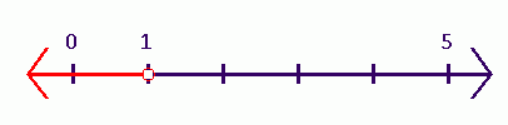
enter image source here

The open circle on #1# means that #1# is not a solution (but anything less than it is).

Hope this helps!