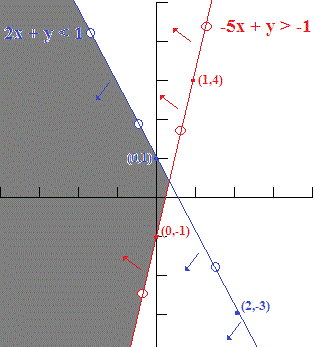
How do you solve #-5x + y > -1 # and #2x + y < 1#?
1 Answer
Jul 31, 2015
This could be re-written as a single compound inequality:
or it could be expressed as a graph (see below)
Explanation:
We could pick a few data points along the corresponding equalities and use these to graph the combination of the inequalities: