How do you solve #6x^2-5x-4<=0#?
1 Answer
May 5, 2015
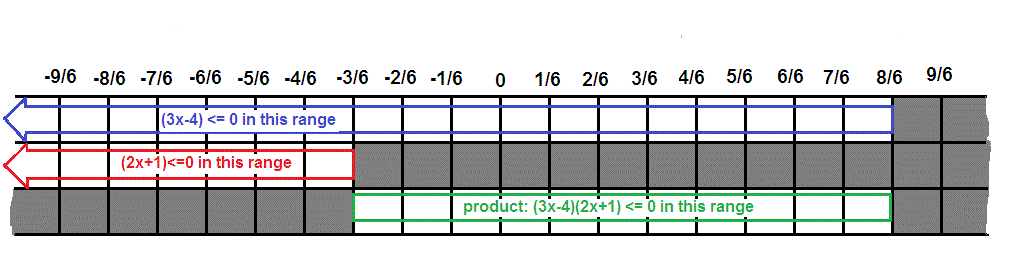
It is fairly easy to factor the left side of this inequality
becomes
The trick is in seeing what this means.
For this to be true
either
or
BUT NOT both