How do you solve #-6z-14>-32# and graph the solution on a number line?
2 Answers
See explanation for number line
Explanation:
First, solve for
Add
When you divide both sides by
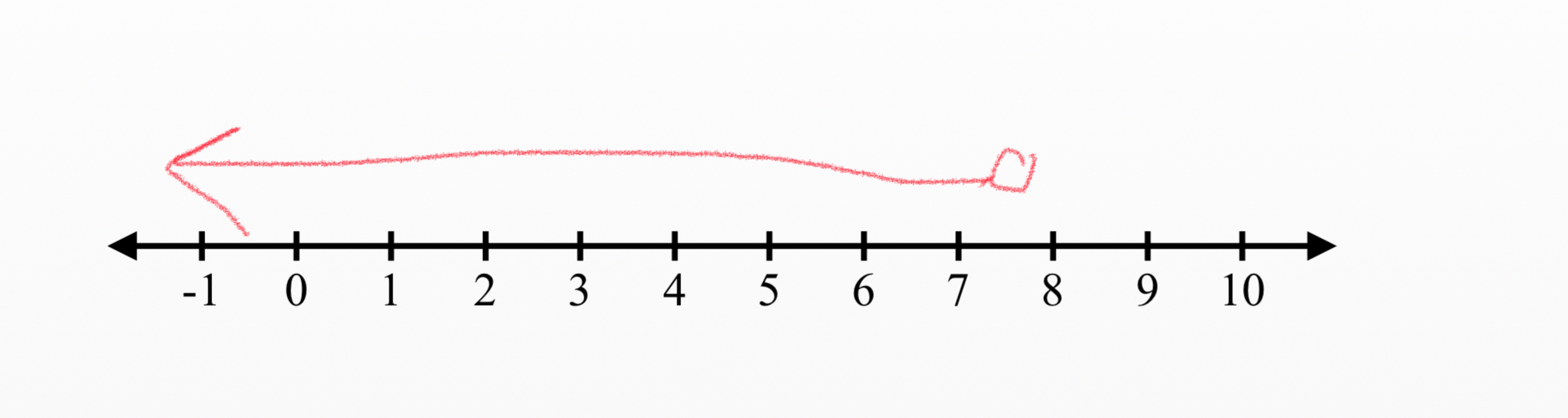
This is what it looks like on a number line (notice the dot that is above
See a solution process below:
Explanation:
First, add
Now, divide each side of the inequality by
Or
To graph this we will draw an open circle at
We will the draw an arrow to the left of the circle because the inequality operator does contain a "less than" clause:


