How do you solve #abs(x-1/3)-2=1?#?
2 Answers
Explanation:
As
hence either
or
Graphically this solution can be plotted as the intersection points of the functions on the LHS and the RHS as shown below :-
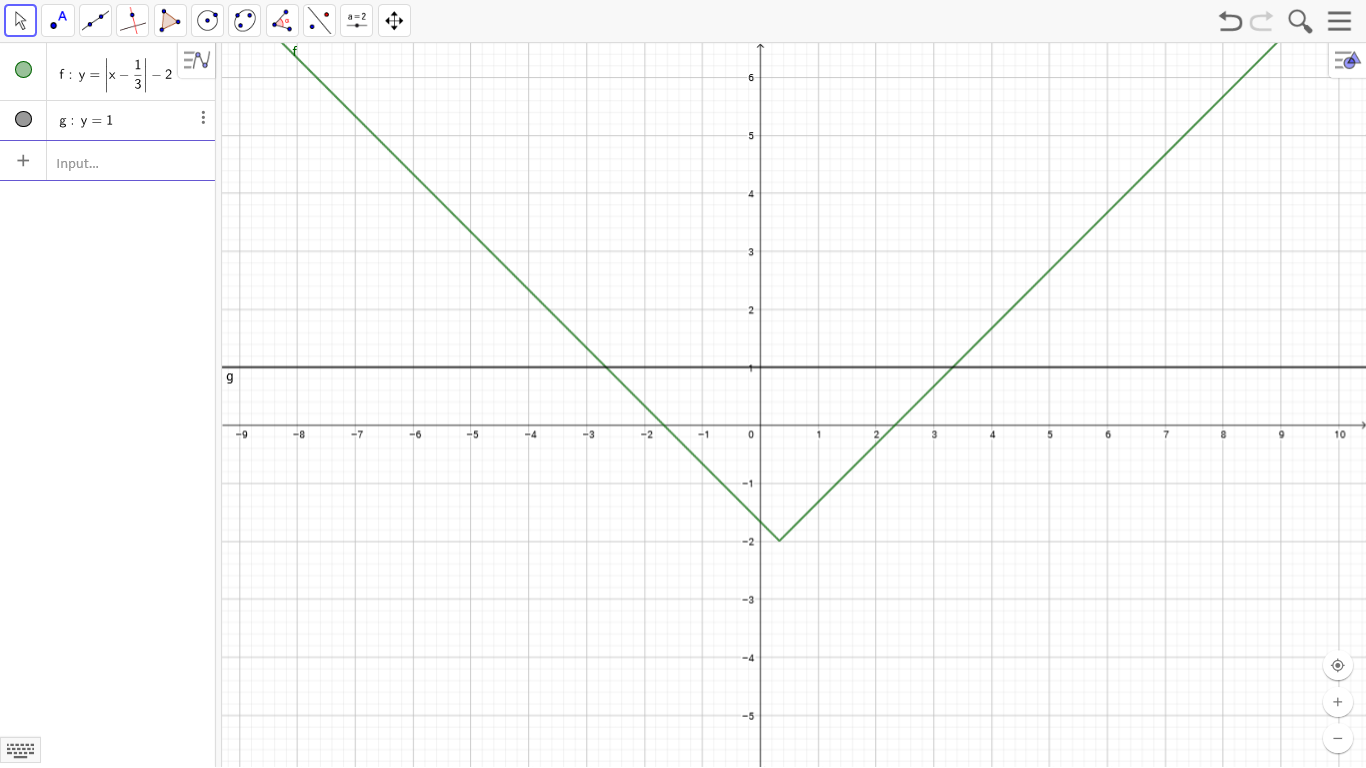 GeoGebra Classic app
GeoGebra Classic app
Explanation:
Any algebraic problem with absolute values you always have to isolate the absolute value on one side of the equation.
In this case:
remember that for absolute values you will have 2 answers because both positive and negative values have a positive absolute value:
Solve for x:
Graphically this solution can be plotted as the intersection points of the functions on the LHS and the RHS as shown below :-
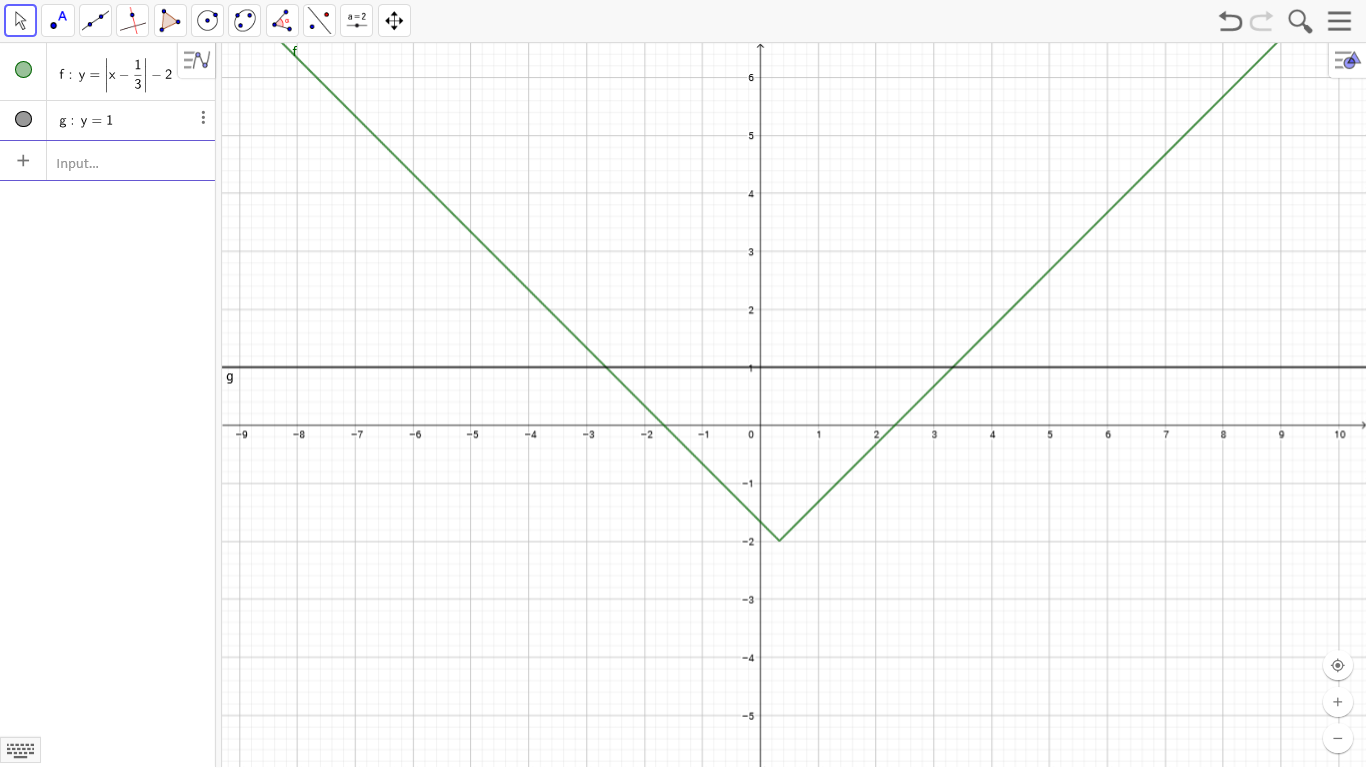 GeoGebra Classic app
GeoGebra Classic app


