First, subtract #color(red)(1)# from each segment of the system of inequalities to isolate the #n# term while keeping the system balanced:
#-2 - color(red)(1) < -2n + 1 - color(red)(1) <= 7 - color(red)(1)#
#-3 < -2n + 0 <= 6#
#-3 < -2n <= 6#
Now, divide each segment of the system by #color(blue)(-2)# to solve for #n# while keeping the system balanced. However, because we are multiplying or dividing inequalities by a negative number we must reverse the inequality operators:
#(-3)/color(blue)(-2) color(red)(>) (-2n)/color(blue)(-2) color(red)(>=) 6/color(blue)(-2)#
#3/2 color(red)(>) (color(blue)(cancel(color(black)(-2)))n)/cancel(color(blue)(-2)) color(red)(>=) -3#
#3/2 color(red)(>) n color(red)(>=) -3#
Or
#n < 3/2# and #n >= -3#
Or, in interval notation:
#[-3, 3/2]
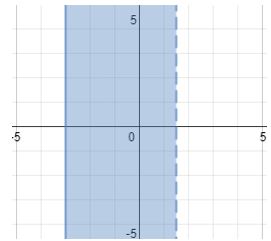
To graph this we will draw a vertical lines at #-3# and #3/2# on the horizontal axis.
The line at #-3# will be a solid line because the inequality operator contains an "or equal to" clause.
The line at #3/2# will be a dashed line because the inequality operator does contains an "or equal to" clause and therefore the line is not part of the solution set.
We will shade between the two lines: