How do you solve the compound inequality #-20≤-6m-2≤58# and graph its solution?
1 Answer
Apr 22, 2015
Break up the given compound inequality
Inequality 1:
inequality 2:
-6m-2<= 58#
Synthesis:
Graph Solution:
This is somewhat more problematic since we don't really have an equation to graph. I suppose you could draw a number line and indicate the range along it...
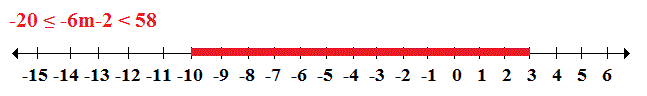
or identify
