How do you solve and graph #2x - (x - 5) - 8 > 3 + 2x#?
2 Answers
Explanation:
Remember that you can add or subtract the same amount from both sides of an inequality without effecting the validity or orientation of the inequality.
(The last step requires recognizing that
...and here it is graphed on a number line:
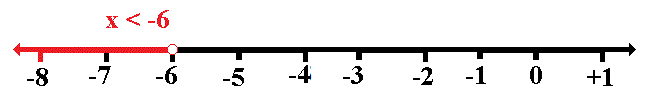
See a solution process below:
Explanation:
First, expand the terms in parenthesis being careful to manage the signs correctly:
Next, combine like terms on the left side of the inequality:
Now, subtract
We can reverse or "flip" the entire inequality to state the solution in terms of
To graph this we will draw a vertical line at
The line will be a dashed line because the inequality operator does not contain an "or equal to" clause and therefore the line is not part of the solution set.
We will shade to the left side of the line because the inequality operator also contains a "less than" clause:
graph{x < -6 [-15, 15, -7.50, 7.50]}

