First, subtract #color(red)(4)# from each segment of the system of inequalities to isolate the #c# term while keeping the system balanced:
#-3 - color(red)(4) <= 7c + 4 - color(red)(4) < 18 - color(red)(4)#
#-7 <= 7c + 0 < 14#
#-7 <= 7c < 14#
Now, divide each segment by #color(red)(7)# to solve for #c# while keeping the system balanced:
#-7/color(red)(7) <= (7c)/color(red)(7) < 14/color(red)(7)#
#-1 <= (color(red)(cancel(color(black)(7)))c)/cancel(color(red)(7)) < 2#
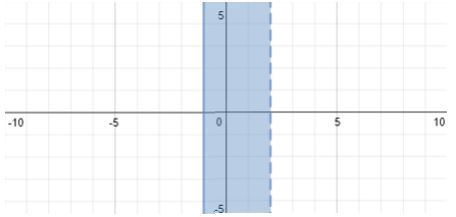
#-1 <= c < 2#
Or
#c >= -1# and #c < 2#
Or, in interval notation:
#[-1, 2)#
To graph this we will draw vertical lines at #-1# and #2# on the horizontal axis.
The line at #-1# will be a solid line because the inequality operator contains an "or equal to" clause. The line at #2# will be a dashed line because the inequality operator does not contain an "or equal to" clause.
We will shade between the lines to show the interval: