How do you solve and graph the compound inequality #4 < n + 6 < 9# ?

1 Answer
Somebody N.
Mar 22, 2018

See below.

Explanation:

#4 < n+6 < 9#

Subtract 6 from each part of the inequality:

#4 -6< n+6-6 < 9-6#

#color(blue)(-2 < n < 3)#

To graph:

Make two equations:

We have:

#n> -2# , #n+2>0#

Equation #y=n+2#

#n < 3 # , #n-3 < 0#

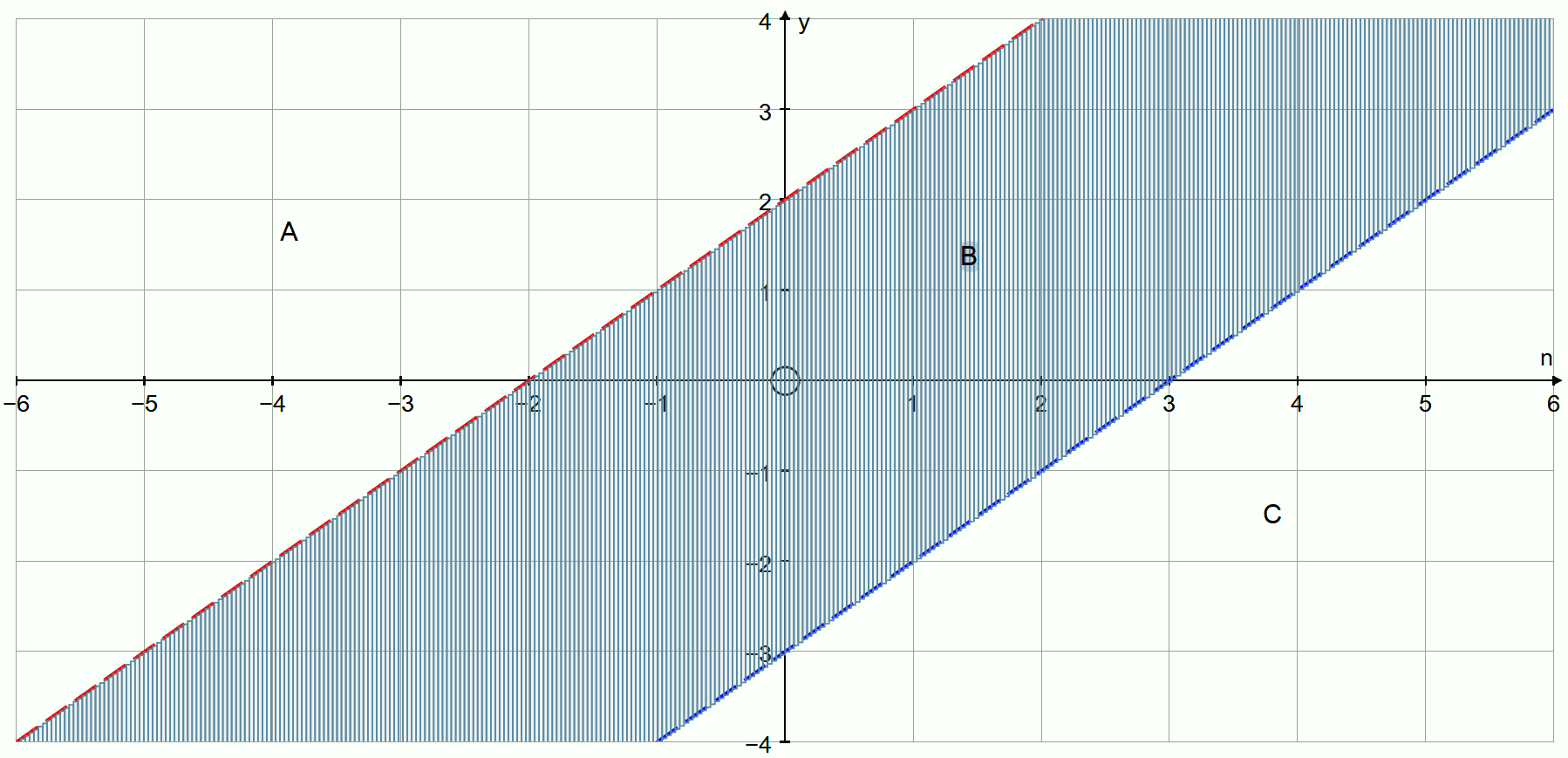
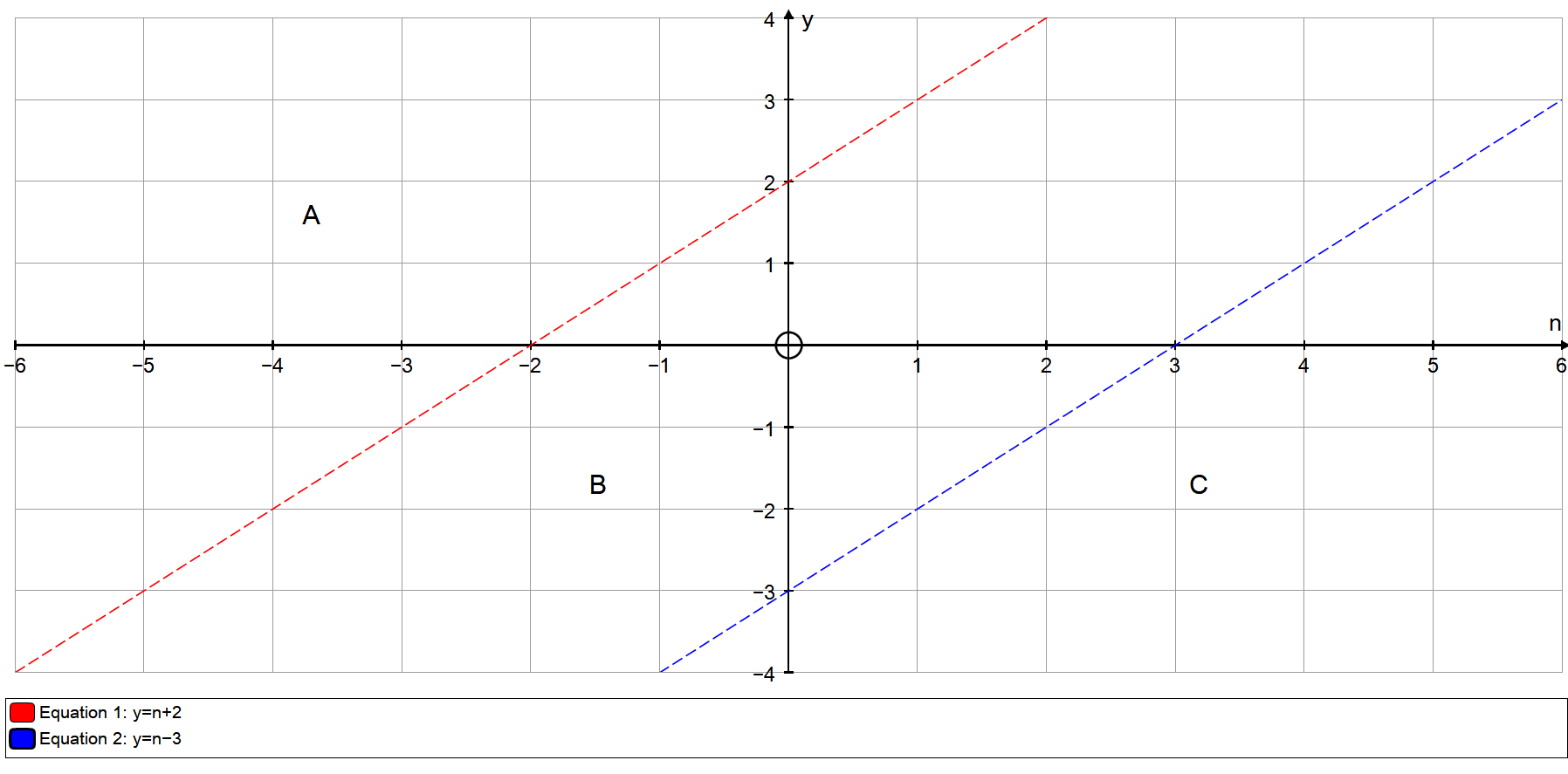
Graph these two lines. This we give you the boundary between included and excluded regions. Remember to use a dotted line as these are of the for < , > and not of the form #<= , >=#, so the line will not be an included region.

With these plotted, we have three regions A , B and C, we now test coordinates in each region to see which is an included or excluded region.

enter image source here

Region A:

coordinates:

#(-3,2)#

#n+2 > y#

#(-3)+2 > 2 \ \ \ \ \ \ \ \ # False

#n-3 < y#

#(-3)-3 < 2 \ \ \ \ \ \ \ \ # True

Region B:

coordinates:

#(2,2)#

#n+2 > y#

#(2)+2 > 2 \ \ \ \ \ \ \ \ # True

#n-3 < y#

#(2)-3 < 2 \ \ \ \ \ \ \ \ # True

Region C

coordinates:

#(-2,4)#

#n+2 > y#

#(-2)+2 > 2 \ \ \ \ \ \ \ \ # False

#n-3 < y#

#(4)-3 < 2 \ \ \ \ \ \ \ \ \ \ \ \ \ # True

The only region where both conditions are met is region B. Shade region B

enter image source here

Related questions
See all questions in Compound Inequalities
Impact of this question
2190 views around the world
You can reuse this answer
Creative Commons License