Question

How do you solve and graph the compound inequality `x- 3 > 3` and `-x + 1 < -2` ?

Answer 1

`" "`
Please read the explanation.

Explanation:

`" "`
We are given the Compound Inequality:

`color(red)((x-3) > 3 " AND " (-x+1)<(-2)`

We can solve these inequalities separately.

Since `color(red)(" AND ")` is used to Join the two inequalities,
the final result will be the intersection of the two given inequalities.

Inequality-1

`(x-3) > 3`

Add `color(red)(3` to both sides of the inequality.

`rArr (x-3)+3>3+3`

`rArr x-cancel 3+cancel 3>3+3`

`rArr x>6` ...Res.1

Inequality-2

`(-x+1)<(-2)`

Subtract `color(red)((-1)` from both sides of the inequality.

`rArr (-x+1)-1<(-2)- 1`

`rArr -x+ cancel 1- cancel 1<-2- 1`

`rArr -x< -3`

Multiply both sides of the inequality by `color(red)((-1)` and please remember to reverse the inequality:

`rArr (-x)(-1)>(-3)(-1)`

`rArr x > 3` ... Res.2

Using the intermediate results (Res.1) and (Res.2), we get

`color(blue)(x>6 " AND " x>3`

FINAL SOLUTION:

`color(red)(x>6`

Using Interval Notation:

`color(red)((6,oo)`

Important Note:

Dotted Lines in all the graphs below represent a solution that does not include a certain value, indicated by the dotted line.

Graph.1

Graph of the inequality: `(x-3) > 3`

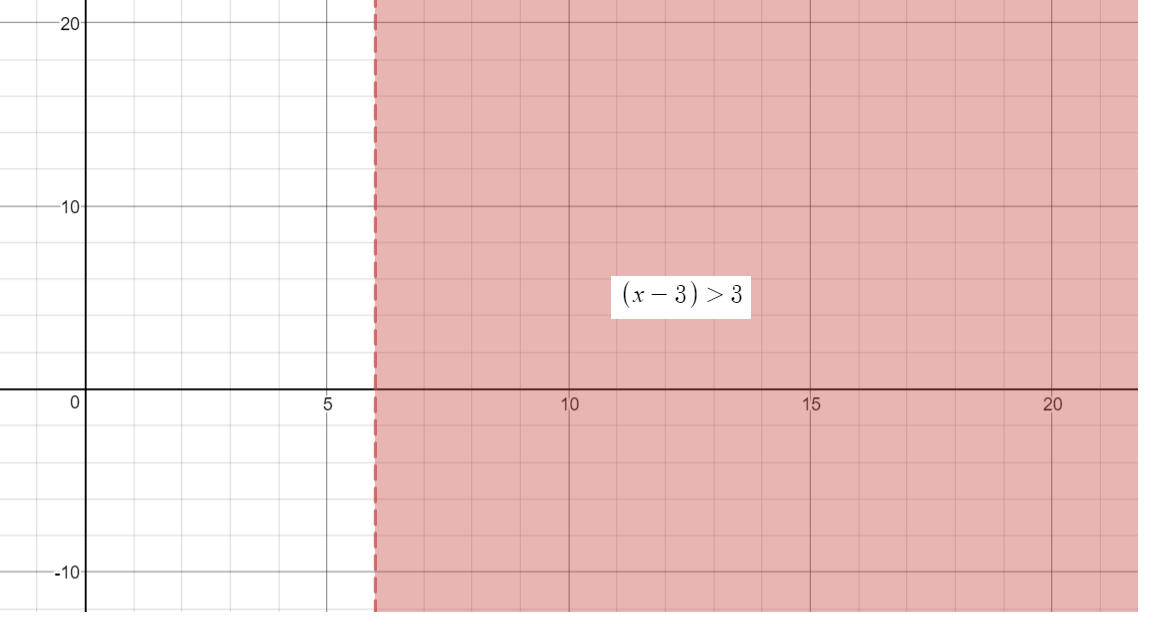
Graph.2

Graph of the inequality: `(-x+1)<(-2)`

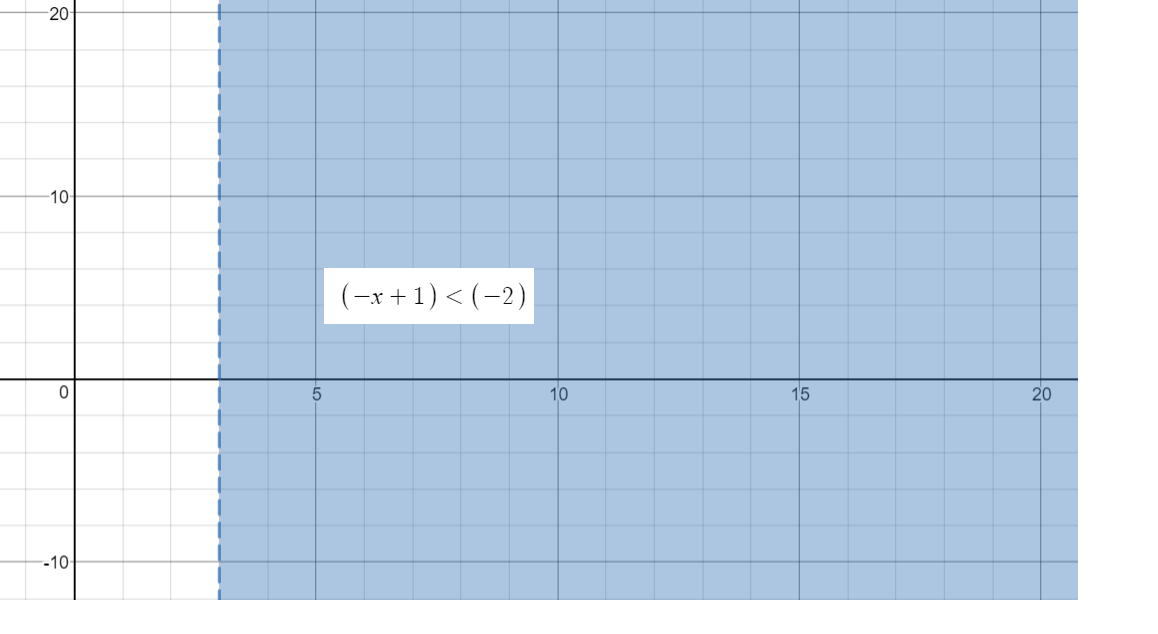
Graph.3: Solution Graph

`color(red)((x-3) > 3 " AND " (-x+1)<(-2)`

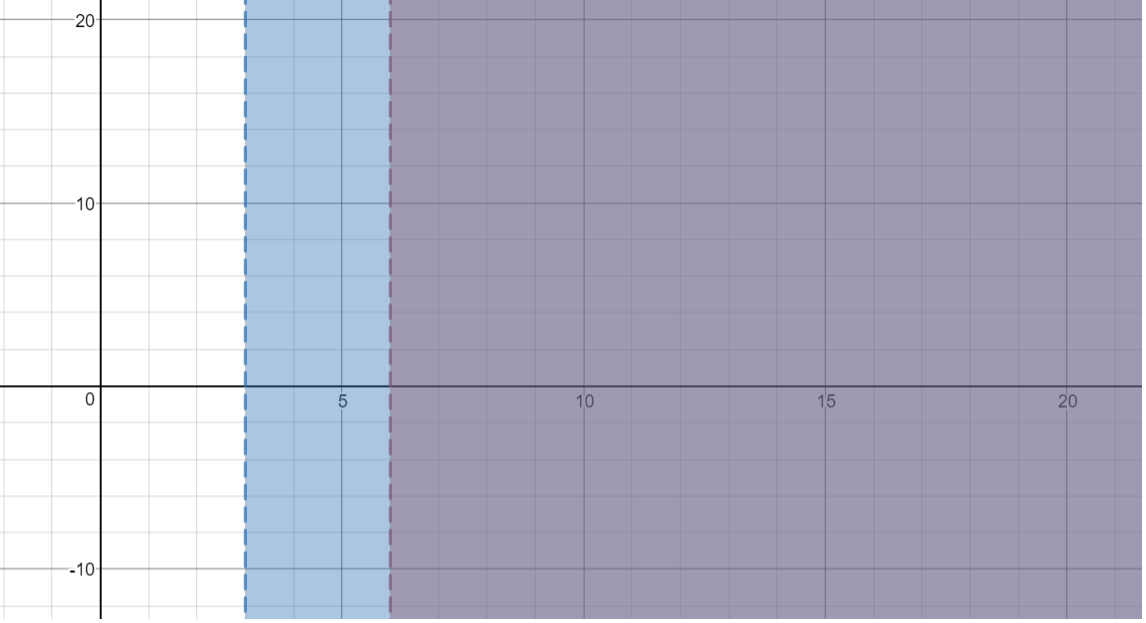
Overlapping area in the graph is our required solution,

Compare this graph with the following graph.

Both the graphs represent the same solution.

Graph.4: Solution Graph `color(red)(x>6`

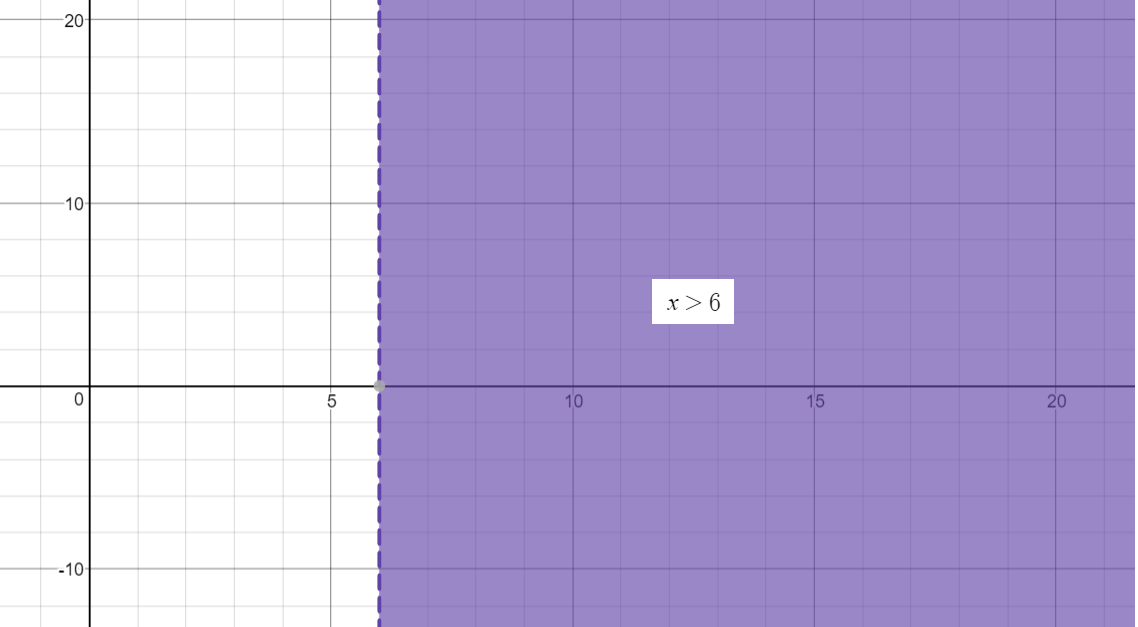
Hope this helps.