First rearrange the inequalities so y is the subject:
#-y+5>=9color(white)(88)# , #color(white)(88)-y >=4# , #color(white)(88)y<=-4#
#3y+4<-5# , #color(white)(88)3y<-9# , #color(white)(88)y<-3#
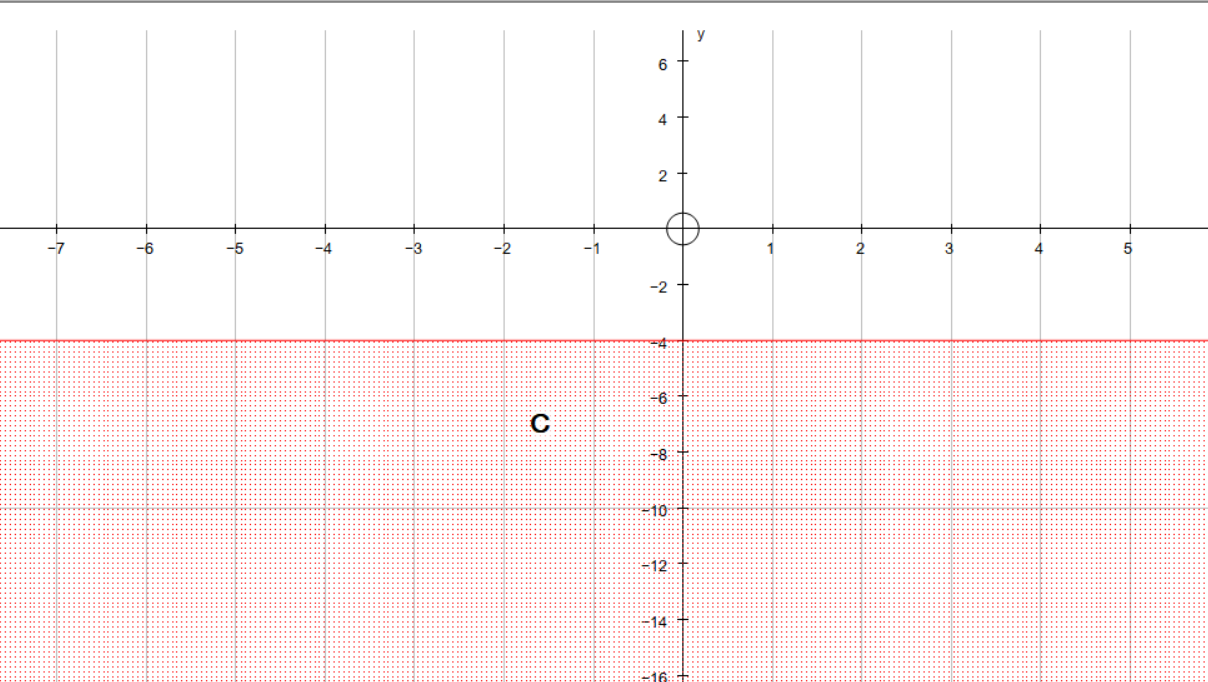
#color(blue)(y<=-4)#
#color(blue)(y<-3)#
Graph these two lines as #y=-4# and #y=-3#. Remember to use a dashed line for #y=-3#, because this is a less than and not a less than or equal to inequality, so the line will not be an included region.
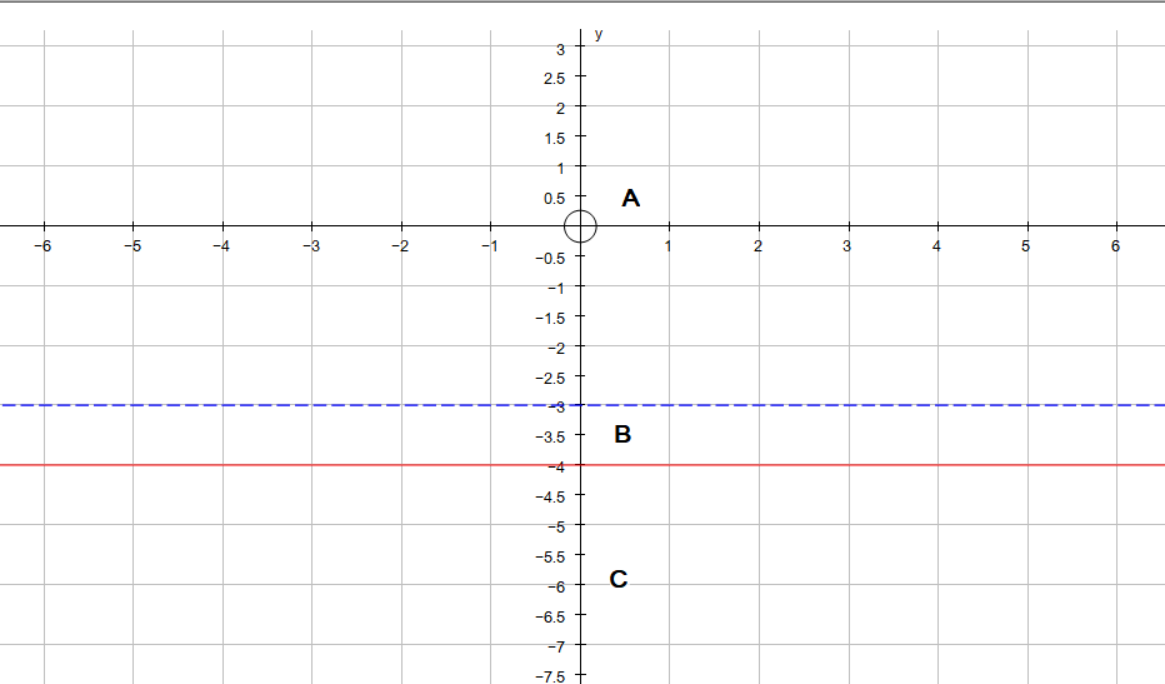
We now need to test #y# values in each region A , B and C. These values have to satisfy both inequalities:
Region A:
#y=-1#
#-1<=-4color(white)(88)# False
#-1<-3color(white)(88)# False
A is not an included region.
Region B:
#y=-3.5#
#-3.5<=-4color(white)(88)#False
#-3.5<-3color(white)(8)# True
Region B is not the included region.
Region C:
#y=-5#
#-5<=-4color(white)(88)#True
#-5<-3color(white)(88)#True
Region C satisfies both, so region C is the included region.