How do you solve and write the following in interval notation: # x^4+4x^3-21x^2>=0#?
2 Answers
Explanation:
but
Explanation:
Factor this to find when the expression is equal to
Factor
#x^2(x^2+4x-21)>=0#
Factor with
#x^2(x+7)(x-3)>=0#
Thus the expression equals
Use one test point in every interval between two pairs of zeros, and another test point between a zero and positive/negative infinities.
Before
We can plug in
#x=-8# into#x^2(x+7)(x-3)# .
#(-8)^2# is positive,#(-8+7)# is negative, and#(-8-3)# is negative, so their product will be positive. Thus the entire interval#(-oo,-7]# will be#>=0# .
Between
Plugging in
#x=-1# yields:
#overbrace((-1)^2)^+overbrace((-1+7))^(+)overbrace((-1-3))^(-) <=0# This is negative, so the interval is not a part of the solution set.
Between
#overbrace((1)^2)^+overbrace((1+7))^(+)overbrace((1-3))^(-) <=0# This is also negative, and not a part of the solution set.
From
Plugging in
#x=4# yields:
#overbrace((4)^2)^+overbrace((4+7))^(+)overbrace((4-3))^+ >=0#
Since this is positive,
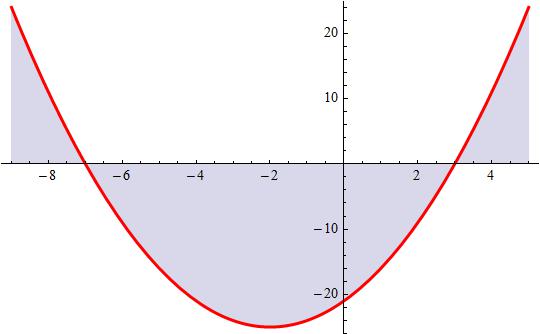
Thus the entire solution is the union of the two positive intervals:
#(-oo,-7]uu[3,+oo)#


