How do you solve and write the following in interval notation: #(x)/(x+1) ≤ (-4)/(3(x-4))#?

Question

2014 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-12-10T23:08:37

See below

#x/(x+1)≤−4/(3(x−4))#

#x/(x+1)+4/(3(x−4))≤0#

#(3x(x-4)+4(x+1))/(3(x+1)(x−4))≤0#

#(3x^2-8x+4)/(3(x+1)(x−4))≤0#

#x_(1,2)=(-b+-sqrt(b^2-4ac))/(2a)#

Let: a=3; b=-8; c=4

#x_(1,2)=(8+-sqrt(8^2-4*3*4))/(2*3)#

#x_(1,2)=(8+-sqrt(16))/(2*3)#

#x_(1,2)=(8+-4)/(2*3)#

#x_1=2/3#

#x_2=2#

#((x-2/3)(x-2))/(3(x+1)(x−4))≤0#

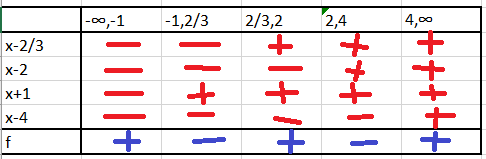
enter image source here

We need to find when is function #<=0#
function is negative for:
#x in (-1,2/3]uuu[2,4)#