Question

How do you solve compound inequalities `p + 4 > 6` and `3p < -18`?

Answer 1

`p+4 > 6 and 3p < -18`
`color(white)("XXXX")` `rArr 2 < p < -6` impossible
There are no values of `p` that satisfy this pair of compound inequalities

Explanation:

Evaluate the two inequalities separately

`p+4 > 6`
`color(white)("XXXX")` `color(white)("XXXX")`Subtract 4 from each side
`color(white)("XXXX")` `p > 2`

`3p < -6`
`color(white)("XXXX")` `color(white)("XXXX")`Divide each side by 3
`color(white)("XXXX")` `color(white)("XXXX")`(this is valid without modifying the orientation of the inequality, since 3 > 0)
`color(white)("XXXX")` `p < -6`

`p+4 > 6` and `3p < -18`
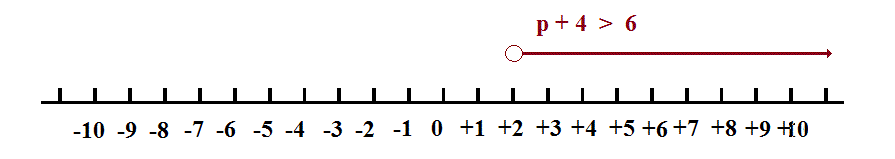
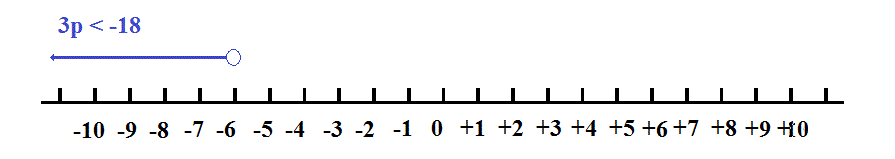
are those values of `p` for which both conditions are true:

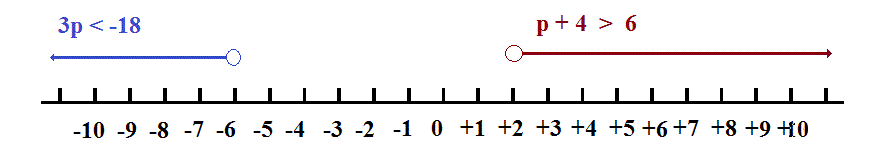
As we can see from the above number line,
there are no values for which both conditions are true.