Question

How do you solve `ln(x)+e^x=0`?

Answer 1

I couldn't find it so I tried with a graphic method...

Explanation:

I tried to plot the right side as a function of `x` to find when it get to zero and I found (approx): `x=0.2699`:

Answer 2

`x~~ 0.27`

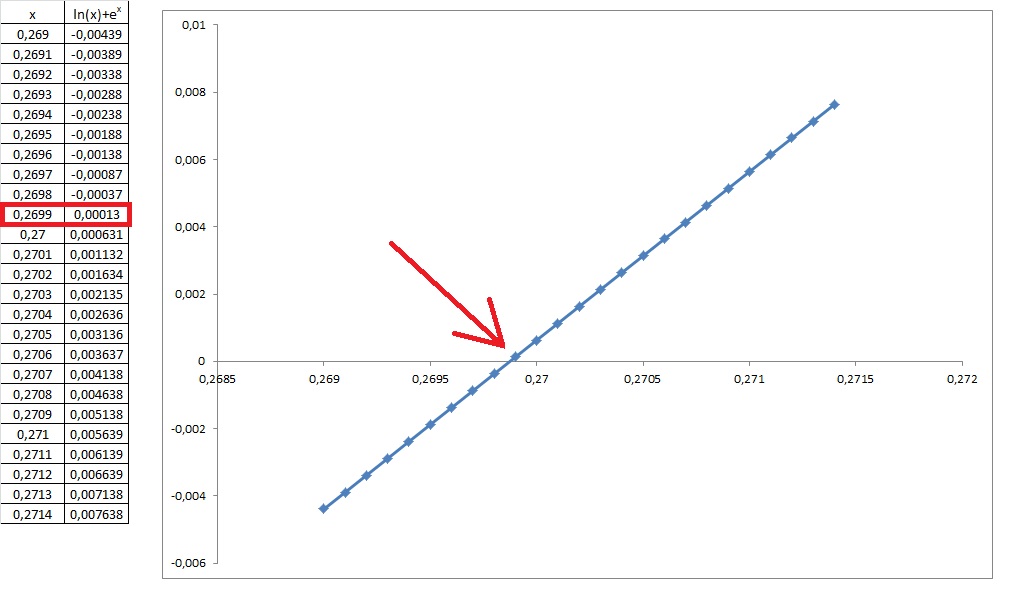
Explanation:

You will need to use a method such as Newton's to derive an approximation.

Beware: This answer will use Calculus

Newton's formula is used to find the roots of equations where algebra cannot be used successfully.

It states

`x_(n + 1) = x_n - f(x_n)/(f'(x_n))`

We start by finding a suitable starting value of `x`. Let's call the function `y = lnx + e^x` `f(x)`.

Then the derivative is given by

`f'(x) = 1/x + e^x`

If we use the initial approximation of `x = 1` (far from a perfect approximation, we should get

`f(x_1) = 0 + e = e`

`f'(x_1) = 1/1 + e = e +1`

The first approximation is given by

`x_(1 + 1) = 1 - e/(e + 1)`

`x_2 = 1 - e/(e + 1)`

This gives a result of `x = 0.27` approximately. We could reapply Newton's method repeatedly, but since the problem doesn't specify, I will leave the answer as that. Note that if you look at the graph of `y = lnx` and `y = -e^x`, check where it intersects, if will give you an intersection point of `x = 0.27`, so at least we're a little close.

Hopefully this helps!