How do you solve mixture problems using system of equations?
1 Answer
Just to make it easier for me, I usually make a small table with the headings "Components", "Unit Value", "Amount" and "Value".
Consider the following question:
How many pints of 20% acid solution and 70% acid solution must be mixed to obtain 40 pints of 50% acid solution?
First, I'll set up my table. I'll fill in the unknowns with variables
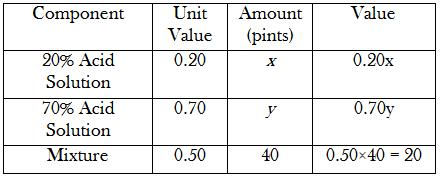
From this, we can easily set up the two equations.
Sum of values of two acids = Value of mixture
Therefore,
For convenience, we'll multiply the entire equation by 10,
This is equation (1)
Setting up the second equation,
Sum of amounts of each acid = Amount of mixture
To make at least one term of this equation identical to a term of equation (1), we'll multiply the entire equation by 2,
This is equation (2)
Subtracting equation (2) from (1),
Thus,
Substituting
So, we have
We can conclude that 16 pints of 20% acid solution must be mixed with 24 pints of 70% solution to obtain 40 pints of 50% solution.
I hope your question was answered.
