Mixture Problems
Key Questions
-
Let's try to think about the general form of a word problem involving mixtures.
In general, we have the following scenario:
- a merchant sells two kinds of products (coffee, sweets, etc).
-
we know the unit prices for both kinds of products and for the final mixture
#p_1# US dollars per pound for the first kind of product,
#p_2# US dollars per pound for the second kind of product
#p_m# US dollars per pound for the mixture -
we know the total quantity formed by the mixture of the two products (
#q# pounds) - we have to find out the quantities of each product needed to form the mixture
(here we have the variables:#x# denoting the quantity of the first kind of product and#y# denoting the quantity of the second kind of product)
Now, we have sufficient information to work out the equations.
First, we know that the sum of the two quantities is
#q# pounds, which gives us the first equation:
#x+y=q# Second, we know that the sale price is the product of quantity and unit price, which gives us the second equation:
#p_1 x + p_2 y = p_m*q# Now, we have a system of two linear equations that can be easily solved by substitution.
-
For mixture problems, the problems usually (but not always) deal with solutions.
When dealing with mixture problems, you need equate the amount of the compound
Here are some examples
- Heating the solution so that some of the water will evaporate and the solution will become more concentrated. Usually, when evaporation is involved, the assumption is that only the water evaporates
Example:
Heating a 500 mL 40% alcohol solution such that the resulting alcohol solution will become a 70% alcohol solution#(0.40)(500) - (0.00)(X) = (0.70)(500 - X)#
- Mixing the solution with the pure form of the compound to increase the concentration
Example:
Mixing a 500 mL 40% alcohol solution with pure alcohol such that the resulting alcohol solution will become a 70% alcohol solution#(0.40)(500) + (1.00)(X) = (0.70)(500 + X)#
- Diluting the solution with water so that the solution will become less concentrated
Example:
Diluting a 500 mL 70% alcohol solution with water such that the resulting alcohol solution will become a 40% alcohol solution#(0.70)(500) + (0.00)(X) = (0.40)(500 + X)#
- Mixing two different concentrations of solution so that the resulting solution will have a concentration that is somewhere in the middle of the two solutions
Example:
Mixing a 500 mL 70% alcohol solution with 40% alcohol solution such that the resulting alcohol solution will become a 50% alcohol solution#(0.70)(500) + (0.40)(X) = (0.50)(500 + X)# -
Just to make it easier for me, I usually make a small table with the headings "Components", "Unit Value", "Amount" and "Value".
Consider the following question:
How many pints of 20% acid solution and 70% acid solution must be mixed to obtain 40 pints of 50% acid solution?
First, I'll set up my table. I'll fill in the unknowns with variables
#x# and#y# .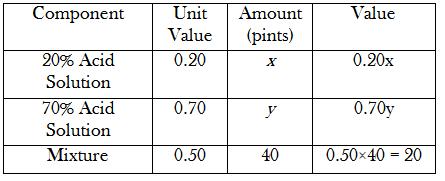
From this, we can easily set up the two equations.
Sum of values of two acids = Value of mixture
Therefore,
#0.20x + 0.70y = 20# For convenience, we'll multiply the entire equation by 10,
#2x + 7y=200# This is equation (1)
Setting up the second equation,
Sum of amounts of each acid = Amount of mixture
#x+y=40# To make at least one term of this equation identical to a term of equation (1), we'll multiply the entire equation by 2,
#2x+2y=80# This is equation (2)
Subtracting equation (2) from (1),
#(+) 2x + 7y=200#
#(-)2x+2y=80#
#--------#
#(=)0+5y=120# Thus,
#5y=120# #y=120/5=24# Substituting
#y=24# in (2),#2x+2(24)=80#
#2x+48=80#
#2x=80-48=32#
#x=32/2=16# So, we have
#x=16# and#y=24# We can conclude that 16 pints of 20% acid solution must be mixed with 24 pints of 70% solution to obtain 40 pints of 50% solution.
I hope your question was answered.