How much of each type should a farmer mix to obtain 100 liters of fertilizer in a 12% solution if he has fertilizer in 5% and 15% solutions?
1 Answer
What we can do here is to apply material balance. What comes in must come out.
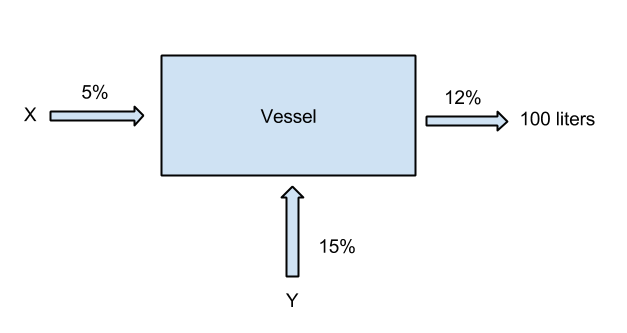
X and Y represents the volume of each fertilizer that the farmers need to mix in order to form 12% of 100 liters of solution.
Observe the arrows pointing to the VESSEL and the arrows pointing away from the VESSEL.
Arrows pointing to the vessel means it goes in.
Arrows pointing away from the vessel means it goes out.
OVERALL MATERIAL BALANCE
What goes in = What comes out
Fertilizer Balance
Simplifying
from
Substitute Y in the fertilizer balance
divide both sides by -0.1
I hope this helped you.

