How do you solve #sec^2x + tanx = 4# in the interval 0 to 2pi?
1 Answer
We will need to use the pythagorean identity
Explanation:
The next part of the solving process requires use of the unit circle.
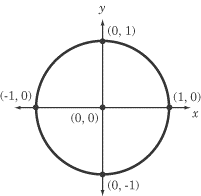
There will be 3 solutions to this equation. Thus, let us break the equation into different parts:
Let's attack the leftmost equation first. As I am sure you know, tan = opposite/adjacent. Since
Now let's attack the other equation.
Here, we need to use the following special triangle. 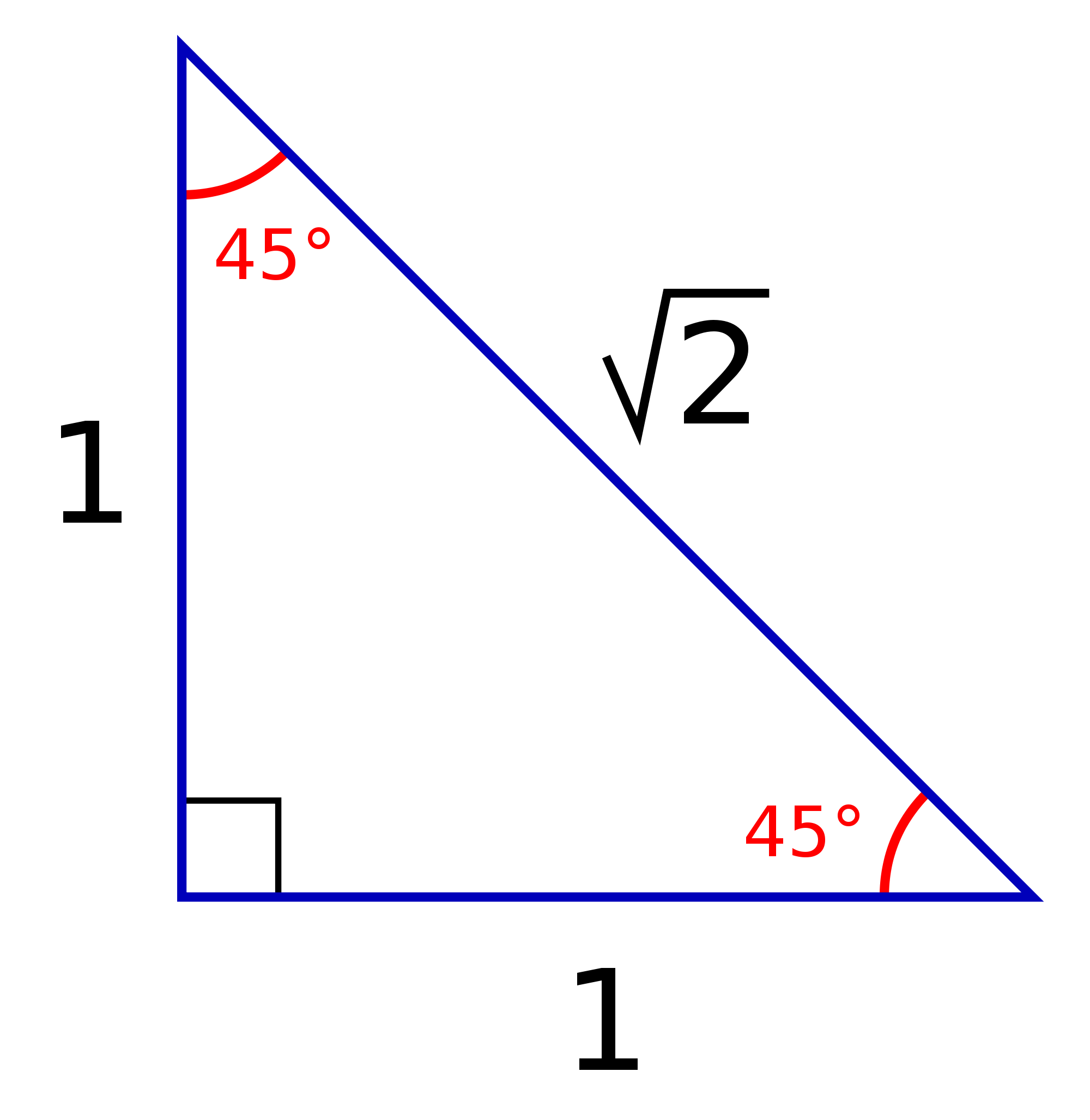
Since we're dealing with tan, which is opposite/adjacent, one and only one of the sides will have to be negative (the ratio would be positive if we had two negative length sides or zero)
We now use our rule C-A-S-T; 4 - 1 - 2 -3, which is meant to show in which quadrants the ratios are positive. By the way, the quadrants are as follows:
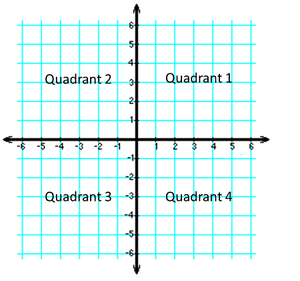
Since tangent is positive in quadrants 1 and 3, it must therefore be negative in quadrants 2 and 4. Finding the reference angle of 45 in quadrants 2 and 4 we get
We must now covert to radian form. This can be done by using the conversion factor
We get:
Finally, many teachers ask for you to present your solution in different forms, one to show the general solution, a regularity since the trigonometric functions repeat themselves in periods and the solution, which is within your range of
solution:
general form: since the period of tan is
Hopefully you understand now. This may seem very foreboding and intimidating at first, but I'm certain you'll get the hang of it.
Have a great night!

