Question

How do you solve `sqrt3cscx-2=0`?

Answer 1

`{x | x = pi/3 + 2kpi, " " x = (2pi)/3 + 2kpi}," " forall k in ZZ`

Explanation:

First, let's isolate `cscx`:

`sqrt3cscx - 2 = 0`

`sqrt3cscx = 2`

`cscx = 2/sqrt3`

Now, since we know that `cscx = 1/sinx`, we can take the reciprocal of both sides of the equation and then solve the equation in terms of `sinx`:

`1/cscx = 1/(2/sqrt3)`

`sinx = sqrt3/2`

Now, we can see that our solution set will be all points where `sinx` is equal to `sqrt3/2`. If we remember our unit circle, we can see that:

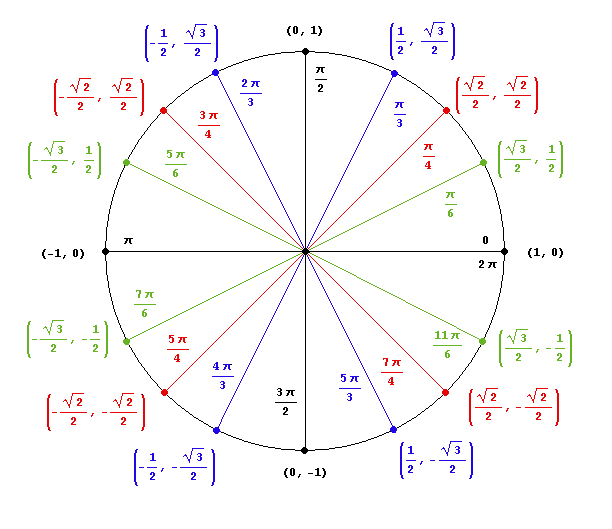
The two points with a y-coordinate of `sqrt3/2` are `x = pi/3` and `x = (2pi)/3`.

Therefore, our solution is:

`{x | x = pi/3, x = (2pi)/3}`

One last touch: remember that the values of all trig functions are the same if you add `2pi` to the angle, so any multiple of `2pi` added to either of these solutions will ALSO be a valid solution of the equation. Therefore, we can represent our final solution set as:

`{x | x = pi/3 + 2kpi, " " x = (2pi)/3 + 2kpi}, " for any integer " k`

Or if you REALLY want to translate the last part into fancy math symbols:

`{x | x = pi/3 + 2kpi, " " x = (2pi)/3 + 2kpi}," " forall k in ZZ`

Final Answer