How do you solve #tan(x+pi)+2sin(x+pi)=0#?

Question

12132 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2016-07-31T01:58:07

For this type of problem, you must use the double angle formulae to expand the parentheses.

The following formulas are extremely important. Be sure to retain them into the future.

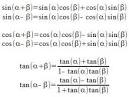
Now, using these formulae, we can expand:

#(tan(x) + tan(pi))/(1 - tanxtanpi) + 2(sinxcospi + cosxsinpi) = 0#

#(tanx + 0)/(1 - tanx xx 0) + 2(sinx(-1) + cosx(0)) = 0#

#tanx/1 + 2(-sinx) = 0#

#tanx - 2sinx = 0#

#sinx/cosx - 2sinx =0#

#(sinx -2sinxcosx)/cosx = 0#

#sinx - 2sinxcosx = 0 xx cosx#

#sinx(1 - 2cosx) = 0#

#sinx = 0 and cosx = 1/2#

#x = 0˚, 180˚, 60˚ and 300˚#

Note that these solutions are only in the interval #0˚ <= x <360˚#.

Hopefully this helps!