How do you solve the equation #x^2+8=-6x# by graphing?
1 Answer
See below.
Explanation:
To graph
First add
We can now write this in function form by replacing the
Find any intercepts ( not the x axis intercepts, since we are going to find them from the graph):
So
We can now find the vertex. This will give us the coordinates of the highest or lowest point on the parabola.
To find the vertex we need to get
Where
To find the vertex:
Bracket off the terms containing the variable:
Factor out the coefficient of
Add the square of half the coefficient of
Change
Collect terms outside the bracket:
This shows that
So the coordinate of the vertex is
To find other points we will have to put in some values for
Examples:
All our coordinates including the vertex and
Plot these points and draw the parabola:
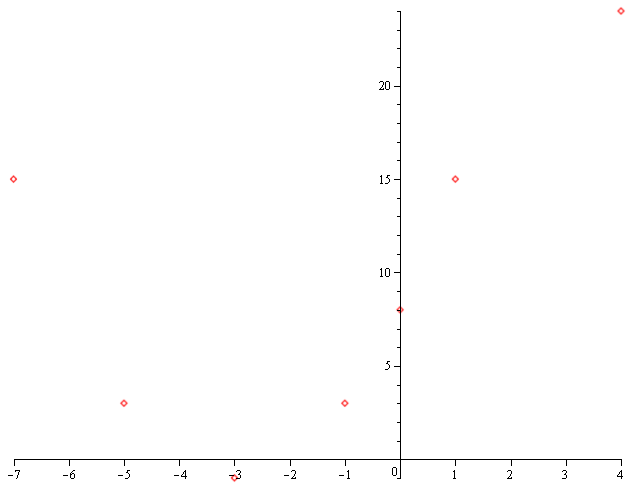
Join points:
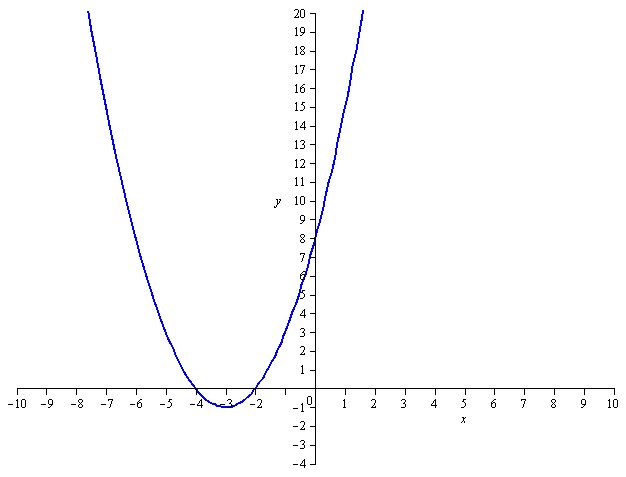
Roots will be where parabola crosses the

