How do you solve the inequality #6x^2-5x>6#?
1 Answer
I would start by solving it as a normal equation (2nd degree). So you write:
Solving your equation you should get two values
Now the tricky bit:
your inequality asks you for values of
They cannot be
Graphically your function gives the following parabola:
graph{6x^2-5x-6 [-11.96, 13.02, -7.14, 5.34]}
So, basically I have to choose values that are outside the boundaries formed by the two values
Consider
If I put
Consider now
If I put
So, OUTSIDE the interval bound by
You express this by writing your solution as:
Or graphically
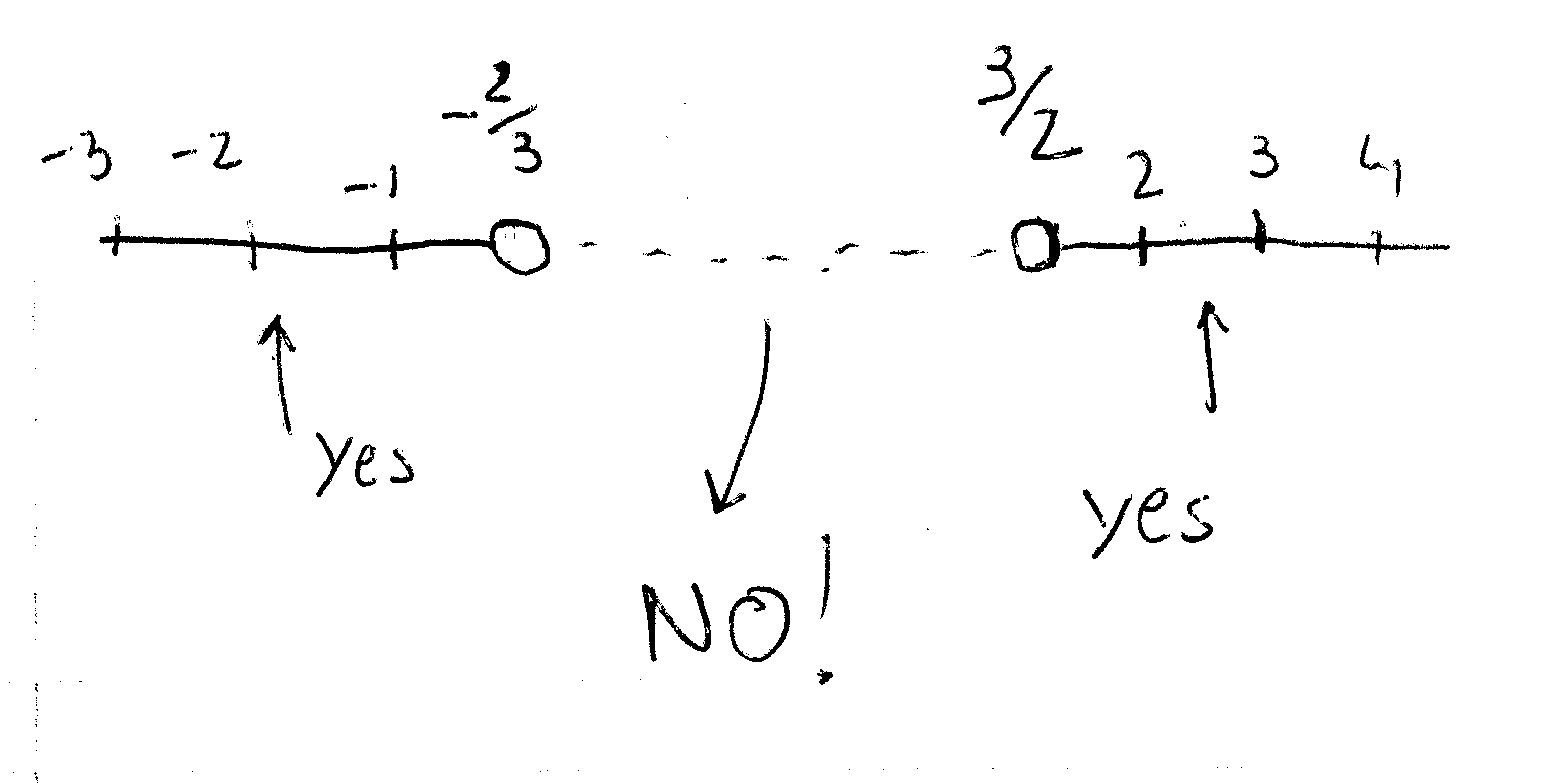
Hope it helps

