Polynomial Inequalities
Key Questions
-
They forget to flip the sign of the inequality when they multiply or divide by a negative number.
-
I use what is called the "test point method" to solve polynomial inequalities.
Ex: (x-3)(x+2) > 0
The factors on the left and the 0 on the right should remind you of the Zero Product Property. In this inequality, we are looking for products that are positive, and not equal to zero.
Since the values of x = 3 and x = -2 both produce zeros, I put those onto a number line and leave open circles to mean that they are not included in the solution set.
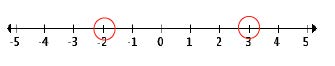
Next, test values between and on the outsides of these two points to see if you get a true statement:
Ex: test -3 (-3-3)(-3+2) = negative times negative = positive (TRUE)
Ex: test 0 (0-3)(0+2) = negative times positive = negative (FALSE)
Ex: test 4 (4-3)(4+2) = positive times positive = positive (TRUE)
and shade your number line accordingly:
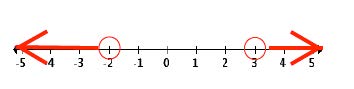
Last, I have my students write their solution sets in interval notation.
#(\infty,-2)U(3,\infty)# The above process will be the same for polynomials of larger degree and more factors. Find a tough one and try it!