How do you solve the triangle ABC given A=30, b=4, c=6?
1 Answer
Feb 20, 2017
Explanation:
You would apply the cosine theorem to find the third side a:
Then
To find the angle
or
then
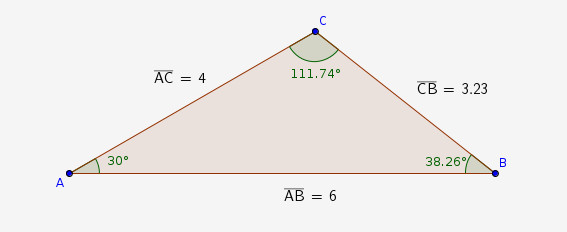
You would apply the cosine theorem to find the third side a:
Then
To find the angle
or
then
