How do you solve the #triangle ABC# given #C=84^circ, c=7, a=2#?
1 Answer
Feb 24, 2018
Explanation:
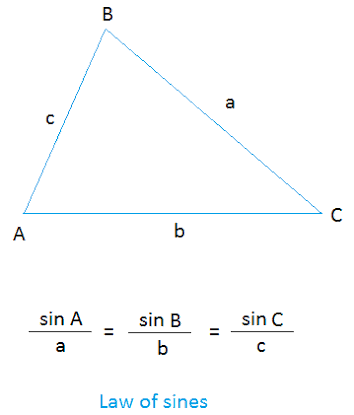
Given :
Applying law of sines,
Sum of the three angles of a triangle equals
Hence

Given :
Applying law of sines,
Sum of the three angles of a triangle equals
Hence