How do you solve the triangle given a = 5, b = 8, c = 12?

Question

10348 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-03-25T07:00:24

#color(green)(A_t = (1/2) a b sin C ~~ 14.52 " sq units)#

We can solve the sum in two ways to find the area of the triangle :

1) Using semi-perimeter formula, having known three sides.

2) By applying law of cosines, we can find one angle and using law of sines we can find the area of the triangle.

Here, we will use Law of cosines and sines and arrive at the area of the triangle.

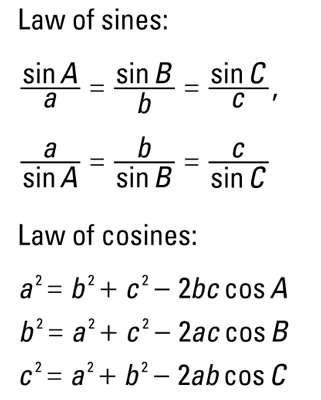
#cos C = (a^2 + b^2 - c^2 ) / (2 * a * b)

#cos C = (5^2 + 8^2 - 12^2) / (2 * 5 * 8)#

#cos C = -55 / 80 = -11 / 16#

#hat C = 133.43^@#

Now, using Law of sines, we calculate the area.

#color(green)(A_t = (1/2) a b sin C = (1/2) * 5 * 8 * sin 133.43 ~~ 14.52 " sq units)#

Answer 2 · 2018-03-25T07:05:43

#color(red)(A_t = sqrt(s * (s-a) * (s-b) * (s-c)) = 14.52 " sq units"#

We will use semi-perimeter formula to find the area of the triangle.

#"Semi-perimeter " s = (a + b + c) / 2 = (5 + 8 + 12) / 2 = 12.5#

Area of the triangle is given by the formula

#A_t = sqrt(s * (s-a) * (s-b) * (s-c))#

#A_t = sqrt(12. 5 * (12.5 - 5) * (12.5 - 8) * (12.5 - 12))#

#color(red)(A_t = sqrt(12.5 * 7.5 * 4.5 * 0.5) = 14.52 " sq units"#